题目内容
用数学归纳法证明“1+a+a2+…+an+1=
，(a≠1，n∈N*)”时，在验证n=1成立时，左边应该是（ ）
| 1-an+2 |
| 1-a |
| A、1+a+a2 |
| B、1+a+a2+a3 |
| C、1+a |
| D、1 |
考点：数学归纳法
专题：证明题,点列、递归数列与数学归纳法
分析：在验证n=1时，左端计算所得的项．只需把n=1代入等式左边即可得到答案．
解答：
解：用数学归纳法证明“1+a+a2+…+an+1=
，(a≠1，n∈N*)”，
在验证n=1时，把当n=1代入，左端=1+a+a2．
故选：A．
| 1-an+2 |
| 1-a |
在验证n=1时，把当n=1代入，左端=1+a+a2．
故选：A．
点评：本题考查了数学归纳法中的归纳奠基步骤，本题较简单，容易解决．不要把n=1与只取一项混同．
练习册系列答案
相关题目
已知正四面体ABCD的棱长为1，则
•
=（（ ）
| AB |
| CD |
A、-
| ||
B、
| ||
| C、1 | ||
| D、0 |
正三棱锥的三视图如图所示，则其外接球的体积为（ ）
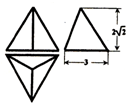
A、9
| ||||
B、
| ||||
| C、18π | ||||
| D、6π |