Question

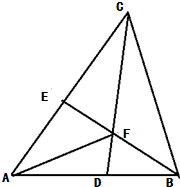在△ABC中，∠A=60°，AB=3，AC=5，BD=1，CE=2．
（1）求BC长；
（2）求

CD

•

BE

的值；
（3）AF与BC是否垂直．

Answer 1

考点：平面向量数量积的运算,空间中直线与直线之间的位置关系

专题：计算题,解三角形,平面向量及应用

分析：（1）运用余弦定理，计算即可得到；
（2）运用向量的三角形法则，以及向量的数量积的定义和性质，计算即可得到；
（3）求出向量AF，由向量AB，AC表示，可由向量的定比公式，计算向量AF，BC的数量积是否为0，即可得到．

解答： 解：（1）由余弦定理可得，
BC²=AB²+AC²-2AB•AC•cos∠BAC
=9+25-2×3×5×

1

2

=19，
即有BC=

19

；
（2）

CD

•

BE

=（

AD

-

AC

）•（

AE

-

AB

）
=（

2

3

AB

-

AC

）•（

3

5

AC

-

AB

）
=

7

5

AB

•

AC

-

2

3

AB

2-

3

5

AC

2
=

7

5

×3×5×

1

2

-

2

3

×9-

3

5

×25=-

21

2

；
（3）令

DF

=λ

FC

，则

AF

=

AD +λ AC

1+λ

=

2 3 AB +λ AC

1+λ

，

BF

=μ

FE

，则

AF

=

AB +μ AE

1+μ

=

AB + 3 5 μ AC

1+μ

，
即有

1 1+μ = 2 3(1+λ) 3μ 5(1+μ) = λ 1+λ

，解得，

λ= 1 2 μ= 5 4

，
则

AF

=

4

9

AB

+

1

3

AC

，

AF

•

BC

=（

4

9

AB

+

1

3

AC

）•（

AC

-

AB

）=

1

3

AC

2-

4

9

AB

2+

1

9

AB

•

AC

=

1

3

×25-

4

9

×9+

1

9

×3×5×

1

2

=

31

6

≠0，
则AF与BC不垂直．

点评：本题考查平面向量的数量积的定义和性质，考查向量垂直的条件和向量的定比公式，考查余弦定理的运用，考查运算能力，属于中档题．