设a=tan35°,b=cos55°,c=sin23°,则( )
| A、a>b>c |
| B、b>c>a |
| C、c>b>a |
| D、c>a>b |
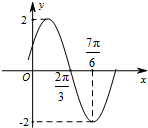 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<| π |
| 2 |
A、f(x)=2sin(2x+
| ||
B、f(x)=2sin(x+
| ||
C、f(x)=2sin(2x+
| ||
D、f(x)=2sin(x+
|
| A、a>b>c |
| B、b>c>a |
| C、c>b>a |
| D、c>a>b |
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<| π |
| 2 |
A、f(x)=2sin(2x+
| ||
B、f(x)=2sin(x+
| ||
C、f(x)=2sin(2x+
| ||
D、f(x)=2sin(x+
|