题目内容
在直角坐标系xoy 中,直线l的参数方程为
,(t为参数).在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点o为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=4cosθ.
(Ⅰ)求圆C在直角坐标系中的方程;
(Ⅱ)若圆C与直线l相切,求实数a的值.
|
(Ⅰ)求圆C在直角坐标系中的方程;
(Ⅱ)若圆C与直线l相切,求实数a的值.
考点:参数方程化成普通方程
专题:选作题,坐标系和参数方程
分析:(I)利用 x=ρcosθ,y=ρsinθ可将圆C的极坐标方程ρ=4cosθ化为普通方程;
(II)据点到直线的距离公式即可求出答案.
(II)据点到直线的距离公式即可求出答案.
解答:
解:(Ⅰ)由ρ=4cosθ得ρ2=4ρcosθ,…(2分)
结合极坐标与直角坐标的互化公式得x2+y2=4x,
即(x-2)2+y2=4 …(5分)
(Ⅱ)由直线l的参数方程为
,化为普通方程,得x-
y-a=0.
结合圆C与直线l相切,得
=2,解得a=-2或6.…(10分)
结合极坐标与直角坐标的互化公式得x2+y2=4x,
即(x-2)2+y2=4 …(5分)
(Ⅱ)由直线l的参数方程为
|
| 3 |
结合圆C与直线l相切,得
| |2-a| |
| 2 |
点评:本题考查极坐标方程化为普通方程、直线与圆相切,理解极坐标方程与普通方程的互化公式和点到直线的距离公式是解决问题的关键.

练习册系列答案
相关题目
在下列函数中,最小值为2的是( )
A、y=
| ||||||
B、y=lgx+
| ||||||
C、y=x+
| ||||||
| D、y=x2-2x+4 |
设a=tan35°,b=cos55°,c=sin23°,则( )
| A、a>b>c |
| B、b>c>a |
| C、c>b>a |
| D、c>a>b |
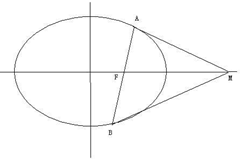 如图,椭圆
如图,椭圆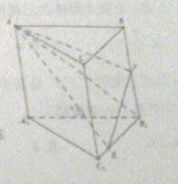 如图,已知三棱柱ABC-A1B1C1中BB1⊥平面ABC,且AC⊥BC1,AA1=3,AC=CB=2.E,F分别为线段B1C1,BB1上的动点.
如图,已知三棱柱ABC-A1B1C1中BB1⊥平面ABC,且AC⊥BC1,AA1=3,AC=CB=2.E,F分别为线段B1C1,BB1上的动点.