题目内容
已知命题P:“对任意x∈[1,2],x2-a≥0”,命题q:“存在x∈R,x2+(a-1)x+1<0”若“p或q”为真,“p且q”为假命题,求实数a的取值范围.
考点:复合命题的真假
专题:简易逻辑
分析:根据二次函数的最值,一元二次不等式解的情况和判别式△的关系即可求出p:a≤1,q:a<-1,或a>3,而根据“p或q”为真,“p且q”为假知道p真q假,或p假q真两种情况,所以求出每种情况的a的取值范围并求并集即可.
解答:
解:由命题p知,x2在[1,2]上的最小值为1,∴p:a≤1;
由命题q知,不等式x2+(a-1)x+1<0有解,∴△=(a-1)2-4>0;
∴a>3或a<-1;
即q:a>3,或a<-1;
∴若“p或q”为真,“p且q”为假,则p,q一真一假;
∴
,或
;
∴-1≤a≤1,或a>3;
∴实数a的取值范围为[-1,1]∪(3,+∞).
由命题q知,不等式x2+(a-1)x+1<0有解,∴△=(a-1)2-4>0;
∴a>3或a<-1;
即q:a>3,或a<-1;
∴若“p或q”为真,“p且q”为假,则p,q一真一假;
∴
|
|
∴-1≤a≤1,或a>3;
∴实数a的取值范围为[-1,1]∪(3,+∞).
点评:考查二次函数在闭区间上的最值,一元二次不等式解的情况和判别式△的关系,以及p或q,p且q的真假和p,q真假的关系.

练习册系列答案
相关题目
在3与27之间插入7个数,使它们成为等差数列,则插入的7个数的第四个数是( )
| A、18 | B、9 | C、12 | D、15 |
在下列函数中,最小值为2的是( )
A、y=
| ||||||
B、y=lgx+
| ||||||
C、y=x+
| ||||||
| D、y=x2-2x+4 |
如图所示,在平行六面体ABCD-A1B1C1D1中,点E为上底面对角线A1C1的中点,若
=
+x
+y
,则( )
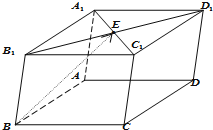
| BE |
| AA1 |
| AB |
| AD |

A、x=-
| ||||
B、x=
| ||||
C、x=-
| ||||
D、x=
|
 如图,平面直角坐标系中,动点P(x,y),PM⊥y轴,垂足为M,点N与点P关于x轴对称,且
如图,平面直角坐标系中,动点P(x,y),PM⊥y轴,垂足为M,点N与点P关于x轴对称,且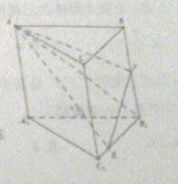 如图,已知三棱柱ABC-A1B1C1中BB1⊥平面ABC,且AC⊥BC1,AA1=3,AC=CB=2.E,F分别为线段B1C1,BB1上的动点.
如图,已知三棱柱ABC-A1B1C1中BB1⊥平面ABC,且AC⊥BC1,AA1=3,AC=CB=2.E,F分别为线段B1C1,BB1上的动点.