题目内容
10.已知a=log35,b=log95,则有( )| A. | a>b>0 | B. | 0<a<b | C. | a<b<0 | D. | 0>a>b |
分析 利用对数函数的单调性即可得出.
解答 解:∵a=log35>1>log95=b>0,
则a>b>0.
故选:A.
点评 本题考查了对数函数的单调性,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
5.已知一个几何体的三视图如图所示,则该几何体的体积为( )


| A. | $16\sqrt{3}$ | B. | $24\sqrt{3}$ | C. | $\frac{{80\sqrt{3}}}{3}$ | D. | $26\sqrt{3}$ |
15.某地区最近十年粮食需求量逐年上升,下表是部分统计数据:
(1)利用所给数据求年需求量y与年份x之间的线性回归方程$\hat y=\hat bx+\hat a$.
(2)利用(1)中所求出的线性回归方程预测该地区2016年的粮食需求量.
(附:$\hat b=\frac{{\sum_{i=1}^n{({x_i}-\bar x)({y_i}-\bar y)}}}{{\sum_{i=1}^n{{{({x_i}\bar-\bar x)}^2}}}},\hat a=\bar y-\hat b\bar x$)
| 年份x | 2010 | 2011 | 2012 | 2013 | 2014 |
| 需求量y万吨 | 236 | 246 | 257 | 276 | 286 |
(2)利用(1)中所求出的线性回归方程预测该地区2016年的粮食需求量.
(附:$\hat b=\frac{{\sum_{i=1}^n{({x_i}-\bar x)({y_i}-\bar y)}}}{{\sum_{i=1}^n{{{({x_i}\bar-\bar x)}^2}}}},\hat a=\bar y-\hat b\bar x$)
20.已知函数f(x)=$\left\{\begin{array}{l}{(lnx)^{2}+alnx+b,x>0}\\{{e}^{x}+\frac{1}{4},x≤0}\end{array}\right.$,且f(e)=f(1),f(e2)=f(0)+$\frac{11}{4}$,则函数f(x)的值域为( )
| A. | ($\frac{1}{4}$,$\frac{5}{4}$]∪($\frac{7}{4}$,+∞) | B. | ($\frac{1}{4}$,$\frac{7}{4}$) | C. | (-∞,$\frac{1}{4}$]∪[$\frac{5}{4}$,+∞) | D. | ($\frac{1}{4}$,$\frac{5}{4}$]∪[$\frac{7}{4}$,+∞) |
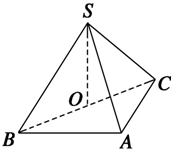 如图所示,在三棱锥S-ABC中,SO⊥平面ABC,侧面SAB与SAC均为等边三角形,∠BAC=90°,O为BC的中点,求二面角A-SC-B的余弦值.
如图所示,在三棱锥S-ABC中,SO⊥平面ABC,侧面SAB与SAC均为等边三角形,∠BAC=90°,O为BC的中点,求二面角A-SC-B的余弦值.