题目内容
20.已知|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{3}$,那么|4$\overrightarrow{a}$-$\overrightarrow{b}$|等于2$\sqrt{3}$.分析 利用两个向量的数量积的定义求得$\overrightarrow{a}•\overrightarrow{b}$的值,再根据|4$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{{(4\overrightarrow{a}-\overrightarrow{b})}^{2}}$,计算求得结果.
解答 解:∵已知|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{3}$,∴$\overrightarrow{a}•\overrightarrow{b}$=1•2•cos$\frac{π}{3}$=1,
∴|4$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{{(4\overrightarrow{a}-\overrightarrow{b})}^{2}}$=$\sqrt{{16\overrightarrow{a}}^{2}-8\overrightarrow{a}•\overrightarrow{b}{+\overrightarrow{b}}^{2}}$=$\sqrt{16-8+4}$=2$\sqrt{3}$,
故答案为:2$\sqrt{3}$.
点评 本题主要考查两个向量的数量积的定义,求向量的模的方法,属于基础题.

练习册系列答案
相关题目
10.已知定义在R上的函数y=f(x)满足函数y=f(x-1)的图象关于直线x=1对称,且当x∈(-∞,0),f(x)+xf'(x)<0成立(f'(x)是函数f(x)的导数),若$a=\frac{1}{2}f({{{log}_2}\sqrt{2}}),b=({ln2})f({ln2}),c=2f({{{log}_{\frac{1}{2}}}\frac{1}{4}})$,则a,b,c的大小关系是( )
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | a>c>b |
8.若$\overrightarrow{a}$=(2,1),$\overrightarrow{b}$=(3,-2),则|2$\overrightarrow{a}$-$\overrightarrow{b}$|=( )
| A. | $\sqrt{17}$ | B. | 1 | C. | $\sqrt{7}$ | D. | $\sqrt{15}$ |
9.已知一个三棱锥的三视图如图所示,则该三棱锥外接球的表面积为( )
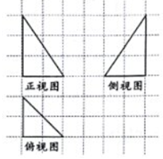

| A. | 17π | B. | 16π | C. | 8π | D. | 20π |
10.已知a=log35,b=log95,则有( )
| A. | a>b>0 | B. | 0<a<b | C. | a<b<0 | D. | 0>a>b |
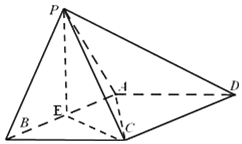 已知四棱锥P-ABCD,底面ABCD为菱形,∠ABC=60°,△PAB是等边三角形,AB=2,PC=$\sqrt{6}$,AB的中点为E
已知四棱锥P-ABCD,底面ABCD为菱形,∠ABC=60°,△PAB是等边三角形,AB=2,PC=$\sqrt{6}$,AB的中点为E