题目内容
18.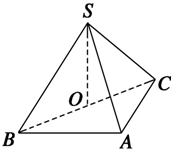 如图所示,在三棱锥S-ABC中,SO⊥平面ABC,侧面SAB与SAC均为等边三角形,∠BAC=90°,O为BC的中点,求二面角A-SC-B的余弦值.
如图所示,在三棱锥S-ABC中,SO⊥平面ABC,侧面SAB与SAC均为等边三角形,∠BAC=90°,O为BC的中点,求二面角A-SC-B的余弦值.
分析 以O为坐标原点,射线OB,OA,OS分别为x轴、y轴、z轴的正半轴,建立如图所示的空间直角坐标系Oxyz.
设B(1,0,0),则C(-1,0,0),A(0,1,0),S(0,0,1),可得<$\overrightarrow{MO}$,$\overrightarrow{MA}$>为二面角A-SC-B的平面角.利用向量求解.
解答 解:以O为坐标原点,射线OB,OA,OS分别为x轴、y轴、z轴的正半轴,
建立如图所示的空间直角坐标系Oxyz.
设B(1,0,0),则C(-1,0,0),A(0,1,0),S(0,0,1),SC的中点M(-$\frac{1}{2}$.0,$\frac{1}{2}$),
故$\overrightarrow{MO}$=(-$\frac{1}{2}$.0,$\frac{1}{2}$),$\overrightarrow{MA}$=($\frac{1}{2}$,1,-$\frac{1}{2}$)$\overrightarrow{SC}$=(-1,0,-1),
所以$\overrightarrow{MO}$•$\overrightarrow{SC}$=0,$\overrightarrow{MA}$•$\overrightarrow{SC}$=0.
即MO⊥SC,MA⊥SC.
故<$\overrightarrow{MO}$,$\overrightarrow{MA}$>为二面角A-SC-B的平面角.
cos<$\overrightarrow{MO}$,$\overrightarrow{MA}$>=$\frac{\overrightarrow{MO}•\overrightarrow{MA}}{|\overrightarrow{MO}||\overrightarrow{MA}|}$=$\frac{\sqrt{3}}{3}$.
即二面角A-SC-B的余弦值为$\frac{\sqrt{3}}{3}$.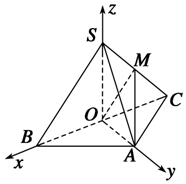
点评 本题考查了向量法求二面角,属于中档题.

| A. | $\sqrt{17}$ | B. | 1 | C. | $\sqrt{7}$ | D. | $\sqrt{15}$ |
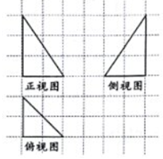
| A. | 17π | B. | 16π | C. | 8π | D. | 20π |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
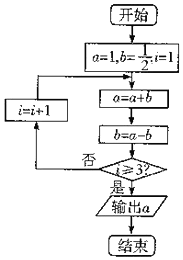
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | a>b>0 | B. | 0<a<b | C. | a<b<0 | D. | 0>a>b |
| A. | $\sqrt{3}$ | B. | $\sqrt{7}$ | C. | 3 | D. | 7 |
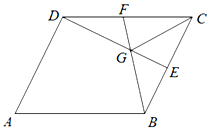 如图,边长为2的菱形ABCD中,∠A=60°,E、F分别是BC、DC的中点,G为 BF、DE的交点,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$.
如图,边长为2的菱形ABCD中,∠A=60°,E、F分别是BC、DC的中点,G为 BF、DE的交点,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$.