题目内容
15.某地区最近十年粮食需求量逐年上升,下表是部分统计数据:| 年份x | 2010 | 2011 | 2012 | 2013 | 2014 |
| 需求量y万吨 | 236 | 246 | 257 | 276 | 286 |
(2)利用(1)中所求出的线性回归方程预测该地区2016年的粮食需求量.
(附:$\hat b=\frac{{\sum_{i=1}^n{({x_i}-\bar x)({y_i}-\bar y)}}}{{\sum_{i=1}^n{{{({x_i}\bar-\bar x)}^2}}}},\hat a=\bar y-\hat b\bar x$)
分析 (1)由所给数据看出,年需求量与年份之间是近似直线上升,利用回归直线方程,对数据预处理,求出预处理后的回归直线方程,从而求出对应的回归直线方程;
(2)利用所求的回归直线方程,计算2016年的粮食需求量即可.
解答 解:(1)由所给数据看出,年需求量与年份之间是近似直线上升,下面来求回归直线方程,先将数据预处理如下:
| 年份-2 012 | -2 | -1 | 0 | 1 | 2 |
| 需求量-257 | -21 | -11 | 0 | 19 | 29 |
由上述计算结果,知所求回归直线方程为$\stackrel{∧}{y}$-257=13(x-2012)+3.2,
即$\stackrel{∧}{y}$=13(x-2012)+260.2;
(2)利用所求得的直线方程,可预测2016年的粮食需求量为
13×(2016-2012)+260.2=13×4+260.2=312.2(万吨).
点评 本题考查了求线性回归方程以及利用回归直线方程预测结果的应用问题,是基础题目.

练习册系列答案
相关题目
6.-400°的终边在哪个象限( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.执行如图所示的程序框图,输出的结果为( )
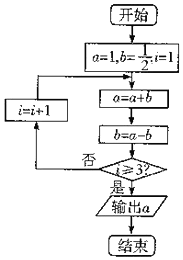

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
10.已知a=log35,b=log95,则有( )
| A. | a>b>0 | B. | 0<a<b | C. | a<b<0 | D. | 0>a>b |
20.用反证法证明命题“若a2+b2=0(a,b∈R),则a,b全为0”,其反设正确的是( )
| A. | a,b至少有一个为0 | B. | a,b至少有一个不为0 | ||
| C. | a,b全部为0 | D. | a,b中只有一个为0 |
7.已知$\overrightarrow a,\overrightarrow b$均为单位向量,并且它们的夹角为120°,那么$|{\overrightarrow a-2\overrightarrow b}|$等于( )
| A. | $\sqrt{3}$ | B. | $\sqrt{7}$ | C. | 3 | D. | 7 |
4.运行如图所示的程序框图,输出i和S的值分别为( )


| A. | 2,15 | B. | 2,7 | C. | 3,15 | D. | 3,7 |
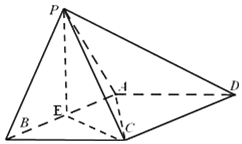 已知四棱锥P-ABCD,底面ABCD为菱形,∠ABC=60°,△PAB是等边三角形,AB=2,PC=$\sqrt{6}$,AB的中点为E
已知四棱锥P-ABCD,底面ABCD为菱形,∠ABC=60°,△PAB是等边三角形,AB=2,PC=$\sqrt{6}$,AB的中点为E