题目内容
19.已知点A(2,3),点B(6,-3),点P在直线3x-4y+3=0上,若满足等式$\overrightarrow{AP}$•$\overrightarrow{BP}$+2λ=0的点P有两个,则实数λ的取值范围是(-∞,2).分析 根据点P在直线3x-4y+3=0上,设P(x,$\frac{3x+3}{4}$),求出$\overrightarrow{AP}$、$\overrightarrow{BP}$,计算$\overrightarrow{AP}$•$\overrightarrow{BP}$,代入$\overrightarrow{AP}$•$\overrightarrow{BP}$+2λ=0,化简并利用△>0求出λ的取值范围.
解答 解:由点P在直线3x-4y+3=0上,设P(x,$\frac{3x+3}{4}$),
则$\overrightarrow{AP}$=(x-2,$\frac{3x+3}{4}$-3),$\overrightarrow{BP}$=(x-6,$\frac{3x+3}{4}$+3),
∴$\overrightarrow{AP}$•$\overrightarrow{BP}$=(x-2)(x-6)+${(\frac{3x+3}{4})}^{2}$-9=$\frac{1}{16}$(25x2-110x+57);
又$\overrightarrow{AP}$•$\overrightarrow{BP}$+2λ=0,
∴$\frac{1}{16}$(25x2-110x+57)+2λ=0,
化简得25x2-110x+57+32λ=0,
根据题意△=(-110)2-4×25×(57+32λ)>0,
解得λ<2;
∴实数λ的取值范围是(-∞,2).
故答案为:(-∞,2).
点评 本题考查了平面向量的数量积与判别式的应用问题,是基础题.

练习册系列答案
相关题目
9.已知一个三棱锥的三视图如图所示,则该三棱锥外接球的表面积为( )
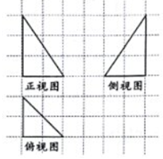

| A. | 17π | B. | 16π | C. | 8π | D. | 20π |
10.已知a=log35,b=log95,则有( )
| A. | a>b>0 | B. | 0<a<b | C. | a<b<0 | D. | 0>a>b |
7.已知$\overrightarrow a,\overrightarrow b$均为单位向量,并且它们的夹角为120°,那么$|{\overrightarrow a-2\overrightarrow b}|$等于( )
| A. | $\sqrt{3}$ | B. | $\sqrt{7}$ | C. | 3 | D. | 7 |
14.运行如图所示的程序框图,若输入的实数为2,则输出的n为( )
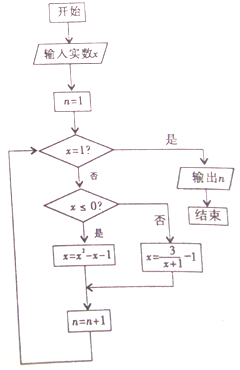

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
4.运行如图所示的程序框图,输出i和S的值分别为( )


| A. | 2,15 | B. | 2,7 | C. | 3,15 | D. | 3,7 |
9.不等式3≤|5-2x|<9的解集为( )
| A. | [-2,1)∪[4,7) | B. | (-2,1]∪[4,7] | C. | (-2,1]∪(4,7) | D. | (-2,1]∪[4,7) |
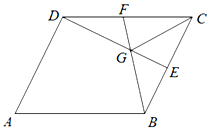 如图,边长为2的菱形ABCD中,∠A=60°,E、F分别是BC、DC的中点,G为 BF、DE的交点,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$.
如图,边长为2的菱形ABCD中,∠A=60°,E、F分别是BC、DC的中点,G为 BF、DE的交点,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$.