题目内容
5.已知一个几何体的三视图如图所示,则该几何体的体积为( )
| A. | $16\sqrt{3}$ | B. | $24\sqrt{3}$ | C. | $\frac{{80\sqrt{3}}}{3}$ | D. | $26\sqrt{3}$ |
分析 利用三视图画出几何体的图形,然后求解几何体的体积即可.
解答 解:该几何体的直观图如图所示,它是一底面是菱形的直四棱柱,
在左上角切去一个三棱锥后形成的几何体.
所以$V=({\frac{1}{2}×4\sqrt{3}×4})×4-\frac{1}{3}({\frac{{\sqrt{3}}}{4}×{4^2}})×4=\frac{{80\sqrt{3}}}{3}$.
故选:C.
点评 本题考查三视图求解几何体的体积,判断几何体的形状是解题的关键.

练习册系列答案
相关题目
16.执行如图所示的程序框图,正确的是( )
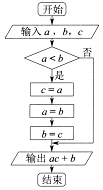

| A. | 若输入a,b,c的值依次为1,2,3,则输出的值为5 | |
| B. | 若输入a,b,c的值依次为1,2,3,则输出的值为7 | |
| C. | 若输入a,b,c的值依次为2,3,4,则输出的值为8 | |
| D. | 若输入a,b,c的值依次为2,3,4,则输出的值为10 |
20.已知命题p:“1,b,4”成等比数列”,命题q:“b=2”,那么p成立是q成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
10.已知a=log35,b=log95,则有( )
| A. | a>b>0 | B. | 0<a<b | C. | a<b<0 | D. | 0>a>b |
17.设双曲线的虚轴长为2,焦距为$2\sqrt{3}$,则双曲线的渐近线方程为( )
| A. | $y=±\sqrt{2}x$ | B. | y=±2x | C. | $y=±\frac{{\sqrt{2}}}{2}x$或y=$±\sqrt{2}x$ | D. | $y=±\frac{1}{2}x$ |
14.运行如图所示的程序框图,若输入的实数为2,则输出的n为( )
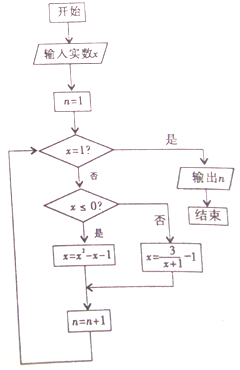

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |