题目内容
已知双曲线
-
=1(a>0,b>0),F是左焦点,A、B分别是虚轴上、下两端,C是它的左顶点,直线AC与直线FB相交于点D,若双曲线的离心率为
,则∠BDA的余弦值等于( )
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:根据离心率为
,得到双曲线是等轴双曲线,然后求出相应直线的倾斜角,利用两角和的余弦公式即可得到结论.
| 2 |
解答:
解:∵双曲线的离心率为
,
∴双曲线是等轴双曲线,即a=b,c=
a,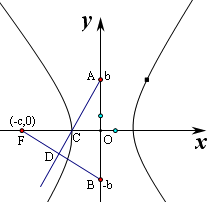
由题意得A(0,b),B(0,-b),C(-a,0),F(-c,0),
即A(0,a),B(0,-a),C(-a,0),F(-
a,0),
则直线AC的方程为
+
=1,即-x+y=a,
则AC的斜率为1,即∠FCD=∠ACx=
,
∵OF=c=
a,OB=b=a,
∴BF=
a,
则sin∠OFB=
=
,cos∠OFB=
=
,
则cos∠BDA=cos(∠OFB+
)=
(cos∠OFB-sin∠OFB)
=
×(
-
)=
,
故选:B
| 2 |
∴双曲线是等轴双曲线,即a=b,c=
| 2 |

由题意得A(0,b),B(0,-b),C(-a,0),F(-c,0),
即A(0,a),B(0,-a),C(-a,0),F(-
| 2 |
则直线AC的方程为
| x |
| -a |
| y |
| a |
则AC的斜率为1,即∠FCD=∠ACx=
| π |
| 4 |
∵OF=c=
| 2 |
∴BF=
| 3 |
则sin∠OFB=
| a | ||
|
| ||
| 3 |
| ||
|
| ||
| 3 |
则cos∠BDA=cos(∠OFB+
| π |
| 4 |
| ||
| 2 |
=
| ||
| 2 |
| ||
| 3 |
| ||
| 3 |
2
| ||||
| 6 |
故选:B
点评:本题主要考查考查三角函数两角和的余弦公式的应用,根据条件确定双曲线是等轴双曲线是解决本题的关键.综合性较强,运算量较大,有一定的难度.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
已知直线l1:ax-2y-1=0,l2:6x-4y+1=0,若l1∥l2,则实数a的值是( )
| A、1 | B、2 | C、3 | D、4 |
回归直线方程的系数a,b的最小二乘法估计中,使函数Q(a,b)最小,Q函数指( )
A、
| |||
B、
| |||
| C、(y1-a-bx1)2 | |||
| D、|y1-a-bx1| |
已知在(1-2x)n的展开式中只有第5项的二项式系数最大且(1-2x)n=a0+a1x+a2x2+…+anxn,则|a1|+|a2|+…+|an|的值为( )
| A、39 |
| B、38 |
| C、39-1 |
| D、38-1 |
在区间[-
,
]上随机取一个数x,则事件“0≤sinx≤1”发生的概率为( )
| π |
| 2 |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=
ax3+
ax2+2a+1的图象经过四个象限,则实数a的取值范围是( )
| 1 |
| 3 |
| 1 |
| 2 |
A、-
| ||||
B、-
| ||||
C、-
| ||||
D、-
|
cos9°cos36°-sin36°sin9°的值为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
