题目内容
甲、乙、丙、丁四人参加某运动会射击项目选拔赛，四人的平均成绩和方差如表所示：
从这四个人中选择一人参加该运动会射击项目比赛，最佳人选是（ ）
| 甲 | 乙 | 丙 | 丁 | |
| 平均环数x | 8.3 | 8.8 | 8.8 | 8.7 |
| 方差ss | 3.5 | 3.6 | 2.2 | 5.4 |
| A、甲 | B、乙 | C、丙 | D、丁 |
考点：极差、方差与标准差,众数、中位数、平均数
专题：概率与统计
分析：丙的射击水平最高且成绩最稳定，故从这四个人中选择一人参加该运动会射击项目比赛，最佳人选是丙．
解答：
解：∵甲、乙、丙、丁四人的平均环数乙和丙均为8.8环，最大，
甲、乙、丙、丁四人的射击环数的方差中丙最小，
∴丙的射击水平最高且成绩最稳定，
∴从这四个人中选择一人参加该运动会射击项目比赛，
最佳人选是丙．
故选：C．
甲、乙、丙、丁四人的射击环数的方差中丙最小，
∴丙的射击水平最高且成绩最稳定，
∴从这四个人中选择一人参加该运动会射击项目比赛，
最佳人选是丙．
故选：C．
点评：本题考查运动会射击项目比赛的最佳人选的确定，是基础题，解题时要认真审题，注意从平均数和方差两个指标进行综合评价．
练习册系列答案
相关题目
已知i为虚数单位，若复数z=1+i，则|z|的值为（ ）
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |
算法语句如图所示：这个算法是用于（ ）
| A、计算3×10的值 |
| B、计算39的值 |
| C、计算1×2×3×…×10的值 |
| D、计算310的值 |
直线
（t为参数）被曲线x2-y2=1截得的弦长是（ ）
|
A、
| ||
B、2
| ||
C、
| ||
D、2
|
已知幂函数y=f（x）的图象过点（2，
），则f（log216）=（ ）
| 2 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
已知双曲线
-
=1（a＞0，b＞0），F是左焦点，A、B分别是虚轴上、下两端，C是它的左顶点，直线AC与直线FB相交于点D，若双曲线的离心率为
，则∠BDA的余弦值等于（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知-
＜θ＜
，且sinθ+cosθ=
，则tanθ的值为（ ）
| π |
| 2 |
| π |
| 2 |
| ||
| 5 |
| A、-3 | ||
B、3或
| ||
C、-
| ||
D、-3或-
|
已知命题p：?x∈R，2x2-1≤0，则￢P：（ ）
| A、?x∈R，2x2-1≤0 |
| B、?x∈R，2x2-1＞0 |
| C、?x∈R，2x2-1≤0 |
| D、?x∈R，2x2-1＞0 |
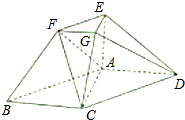在如图所示的几何体中，ABCD为平行四边形，∠ACB=