题目内容
数列{an}的前n项和记为Sn,已知an=
.
(Ⅰ)求S1,S2,S3的值,猜想Sn的表达式;
(Ⅱ)请用数学归纳法证明你的猜想.
| 1 |
| n(n+1) |
(Ⅰ)求S1,S2,S3的值,猜想Sn的表达式;
(Ⅱ)请用数学归纳法证明你的猜想.
考点:数学归纳法,数列递推式
专题:综合题,点列、递归数列与数学归纳法
分析:(1)根据题设条件,可求S1,S2,S3的值,猜想Sn的表达式.
(2)利用数学归纳法的证明步骤对这个猜想加以证明.
(2)利用数学归纳法的证明步骤对这个猜想加以证明.
解答:
解:(Ⅰ)∵an=
,
∴S1=
,S2=
,S3=
,
猜想Sn=
;
(Ⅱ)①n=1时,S1=
成立;
②假设n=k时,成立,即Sk=
,
则当n=k+1时,Sk+1=Sk+ak+1=
+
=
,
即当n=k+1时,结论也成立
综上①②知,Sn=
.
| 1 |
| n(n+1) |
∴S1=
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
猜想Sn=
| n |
| n+1 |
(Ⅱ)①n=1时,S1=
| 1 |
| 2 |
②假设n=k时,成立,即Sk=
| k |
| k+1 |
则当n=k+1时,Sk+1=Sk+ak+1=
| k |
| k+1 |
| 1 |
| (k+1)(k+2) |
| k+1 |
| (k+1)+1 |
即当n=k+1时,结论也成立
综上①②知,Sn=
| n |
| n+1 |
点评:本题主要考查了数列的递推式,考查数学归纳法.数列的递推式是高考中常考的题型,涉及数列的通项公式,求和问题,数列与不等式的综合等问题.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
已知双曲线
-
=1(a>0,b>0),F是左焦点,A、B分别是虚轴上、下两端,C是它的左顶点,直线AC与直线FB相交于点D,若双曲线的离心率为
,则∠BDA的余弦值等于( )
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
圆(x-3)2+y2=4与圆x2+(y-4)2=16的位置关系为( )
| A、内切 | B、外切 | C、相交 | D、相离 |
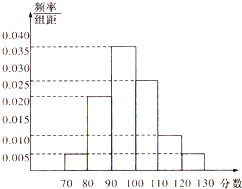 我校高1201、1202、1203、1204四个班,从中随机抽取部分学生进行成绩统计,各班被抽取学生的人数恰好成等差数列,人数最少的班被抽取了24人,抽取的学生的测试成绩统计结果整理得如图所示频率分布直方图,其中分数在[120,130]的人数为6人.
我校高1201、1202、1203、1204四个班,从中随机抽取部分学生进行成绩统计,各班被抽取学生的人数恰好成等差数列,人数最少的班被抽取了24人,抽取的学生的测试成绩统计结果整理得如图所示频率分布直方图,其中分数在[120,130]的人数为6人.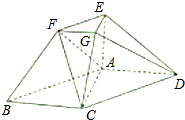 在如图所示的几何体中,ABCD为平行四边形,∠ACB=
在如图所示的几何体中,ABCD为平行四边形,∠ACB=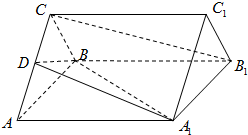 如图,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是
如图,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是