题目内容
已知直线l1:ax-2y-1=0,l2:6x-4y+1=0,若l1∥l2,则实数a的值是( )
| A、1 | B、2 | C、3 | D、4 |
考点:直线的一般式方程与直线的平行关系
专题:直线与圆
分析:利用直线平行的性质求解.
解答:
解:∵直线l1:ax-2y-1=0,l2:6x-4y+1=0,l1∥l2,
∴
=
≠
,
解得a=3.
故选:C.
∴
| a |
| 6 |
| -2 |
| -4 |
| -1 |
| 1 |
解得a=3.
故选:C.
点评:本题考查实数值的求法,是基础题,解题时要认真审题,注意直线平行的性质的灵活运用.

练习册系列答案
相关题目
在等差数列{an}中,若a2=2,a12=12,那么a4+a19=( )
| A、10 | B、23 | C、28 | D、60 |
已知i为虚数单位,若复数z=1+i,则|z|的值为( )
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |
已知定义在实数集R上的函数f(x)满足f(1)=3,且f(x)的导函数f′(x)<2,则不等式f(lnx)<2lnx+1的解集为( )
| A、(1,+∞) |
| B、(e,+∞) |
| C、(0,1) |
| D、(0,e) |
任取一自然数,则该数平方的未位数是6的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知数列{an}是递增数列,且an=
,则t的取值范围是( )
| 2n+t2-8 |
| n+t |
| A、[0,4) |
| B、(0,4) |
| C、[-1,4) |
| D、(-1,4) |
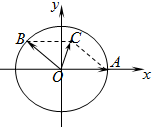 如图,在xOy平面上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π),若
如图,在xOy平面上,点A(1,0),点B在单位圆上,∠AOB=θ(0<θ<π),若