题目内容
cos9°cos36°-sin36°sin9°的值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
考点：两角和与差的正弦函数
专题：三角函数的求值
分析：用两角和公式对原式化简求值．
解答：
解：原式=cos（9°+36°）=cos45°=
，
故选B．
| ||
| 2 |
故选B．
点评：本题主要考查了两角和与差的余弦函数公式的应用．属基础题．
练习册系列答案
相关题目
已知数列{an}是递增数列，且an=
，则t的取值范围是（ ）
| 2n+t2-8 |
| n+t |
| A、[0，4） |
| B、（0，4） |
| C、[-1，4） |
| D、（-1，4） |
已知双曲线
-
=1（a＞0，b＞0），F是左焦点，A、B分别是虚轴上、下两端，C是它的左顶点，直线AC与直线FB相交于点D，若双曲线的离心率为
，则∠BDA的余弦值等于（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
F1，F2是椭圆
+
=1（a＞b＞0）的左、右焦点，若在椭圆上存在点P，且满足|PF1|=2|PF2|，则椭圆的离心率的取值范围为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、[
| ||
B、（
| ||
C、（
| ||
D、（0，
|
已知命题p：?x∈R，2x2-1≤0，则￢P：（ ）
| A、?x∈R，2x2-1≤0 |
| B、?x∈R，2x2-1＞0 |
| C、?x∈R，2x2-1≤0 |
| D、?x∈R，2x2-1＞0 |
数列{an}满足a1=
，an+1=1-
，那么a10=（ ）
| 1 |
| 2 |
| 1 |
| an |
| A、-1 | ||
B、
| ||
| C、1 | ||
| D、2 |
圆（x-3）2+y2=4与圆x2+（y-4）2=16的位置关系为（ ）
| A、内切 | B、外切 | C、相交 | D、相离 |
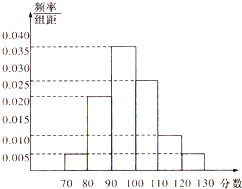我校高1201、1202、1203、1204四个班，从中随机抽取部分学生进行成绩统计，各班被抽取学生的人数恰好成等差数列，人数最少的班被抽取了24人，抽取的学生的测试成绩统计结果整理得如图所示频率分布直方图，其中分数在[120，130]的人数为6人．