题目内容
已知在（1-2x）n的展开式中只有第5项的二项式系数最大且（1-2x）n=a0+a1x+a2x2+…+anxn，则|a1|+|a2|+…+|an|的值为（ ）
| A、39 |
| B、38 |
| C、39-1 |
| D、38-1 |
考点：二项式系数的性质
专题：二项式定理
分析：先求出n=8，a0=1，根据要求的式子即|a0|+|a1|+|a2|+…+|an|-1，即（1+2x）8的展开式各项系数和减去1，令x=1，可得（1+2x）8的展开式各项系数和为38，从而求得结果．
解答：
解：∵在（1-2x）n的展开式中只有第5项的二项式系数
最大，∴n=8．
故所给的等式即 （1-2x）8=a0+a1x+a2x2+…+a8x8，∴a0=1．
则|a1|+|a2|+…+|an|=|a0|+|a1|+|a2|+…+|an|-1，即（1+2x）8的展开式各项系数和减去1．
令x=1，可得（1+2x）8的展开式各项系数和为38，
∴|a1|+|a2|+…+|an|=38-1，
故选：D．
| C | 4 n |
故所给的等式即 （1-2x）8=a0+a1x+a2x2+…+a8x8，∴a0=1．
则|a1|+|a2|+…+|an|=|a0|+|a1|+|a2|+…+|an|-1，即（1+2x）8的展开式各项系数和减去1．
令x=1，可得（1+2x）8的展开式各项系数和为38，
∴|a1|+|a2|+…+|an|=38-1，
故选：D．
点评：本题主要考查二项式定理的应用，注意根据题意，分析所给代数式的特点，通过给二项式的x赋值，求展开式的系数和，可以简便的求出答案，属于基础题．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
在等差数列{an}中，若a2=2，a12=12，那么a4+a19=（ ）
| A、10 | B、23 | C、28 | D、60 |
已知数列{an}是递增数列，且an=
，则t的取值范围是（ ）
| 2n+t2-8 |
| n+t |
| A、[0，4） |
| B、（0，4） |
| C、[-1，4） |
| D、（-1，4） |
已知函数f（x）=
，若f（a）=0，则实数a的值等于（ ）
|
| A、-3 | B、1 |
| C、-3或1 | D、-1或3 |
直线
（t为参数）被曲线x2-y2=1截得的弦长是（ ）
|
A、
| ||
B、2
| ||
C、
| ||
D、2
|
黑白两种颜色的正方形地砖依照如图的规律拼成若干个图形，现将一粒豆子随机撒在第10个图中，则豆子落在白色地砖上的概率是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
已知双曲线
-
=1（a＞0，b＞0），F是左焦点，A、B分别是虚轴上、下两端，C是它的左顶点，直线AC与直线FB相交于点D，若双曲线的离心率为
，则∠BDA的余弦值等于（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
F1，F2是椭圆
+
=1（a＞b＞0）的左、右焦点，若在椭圆上存在点P，且满足|PF1|=2|PF2|，则椭圆的离心率的取值范围为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、[
| ||
B、（
| ||
C、（
| ||
D、（0，
|
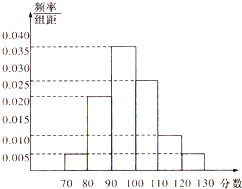我校高1201、1202、1203、1204四个班，从中随机抽取部分学生进行成绩统计，各班被抽取学生的人数恰好成等差数列，人数最少的班被抽取了24人，抽取的学生的测试成绩统计结果整理得如图所示频率分布直方图，其中分数在[120，130]的人数为6人．