题目内容
若f(x)=x3-6ax在区间(-2,2)上单调递减,则a的取值范围为 .
考点:利用导数研究函数的单调性
专题:导数的概念及应用
分析:由函数f(x)=x3-6ax在(-2,2)内单调递减转化成f'(x)≤0在(-2,2)内恒成立,利用参数分离法即可求出a的范围.
解答:
解:解:∵函数f(x)=x3-6ax在(-2,2)内单调递减,
∴f'(x)=3x2-6a≤0在(-2,2)内恒成立.
即 a≥
x2在(-2,2)内恒成立.
∴a≥
×4=2
故答案为:[2,+∞).
∴f'(x)=3x2-6a≤0在(-2,2)内恒成立.
即 a≥
| 1 |
| 2 |
∴a≥
| 1 |
| 2 |
故答案为:[2,+∞).
点评:此题主要考查利用导函数的正负判断原函数的单调性,属于基础题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
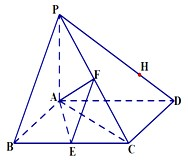 四棱锥P-ABCD底面是菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
四棱锥P-ABCD底面是菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点. 已知正方体ABCD-A1B1C1D1的各棱长为2,则D1到面AB1C的距离为
已知正方体ABCD-A1B1C1D1的各棱长为2,则D1到面AB1C的距离为
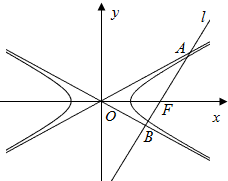 如图所示,已知双曲线
如图所示,已知双曲线