题目内容
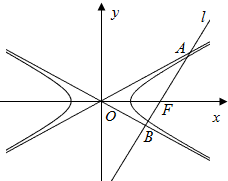 如图所示,已知双曲线
如图所示,已知双曲线| x2 |
| a2 |
| y2 |
| b2 |
| AF |
| FB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:先求出直线l的方程为y=
(x-c),与y=±
x联立,可得A,B的纵坐标,利用
=2
,求出a,b的关系,即可求出该双曲线的离心率.
| 2ab |
| a2-b2 |
| b |
| a |
| AF |
| FB |
解答:
解:双曲线
-
=1(a>b>0)的渐近线方程为y=±
x,
∵直线l的倾斜角是渐近线OA倾斜角的2倍,
∴kOA=
=
,
∴直线l的方程为y=
(x-c),
与y=±
x联立,可得y=-
或y=
,
∵
=2
,
∴
=2•(
),
∴a=
b,
∴c=2b,
∴e=
=
.
故选:B.
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
∵直线l的倾斜角是渐近线OA倾斜角的2倍,
∴kOA=
| ||
1-
|
| 2ab |
| a2-b2 |
∴直线l的方程为y=
| 2ab |
| a2-b2 |
与y=±
| b |
| a |
| 2abc |
| 3a2-b2 |
| 2abc |
| a2+b2 |
∵
| AF |
| FB |
∴
| 2abc |
| a2+b2 |
| 2abc |
| 3a2-b2 |
∴a=
| 3 |
∴c=2b,
∴e=
| c |
| a |
2
| ||
| 3 |
故选:B.
点评:本题考查双曲线的简单性质,考查向量知识,考查学生的计算能力,属于中档题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
设a>0,b>0,若
是2a与b的等比中项,则
+
的最小值为( )
| 2 |
| 1 |
| a |
| 1 |
| b |
| A、2 | B、4 | C、8 | D、16 |
设集合U=R,集合M={x|x>1},P={x|x2>1},则下列关系正确的是( )
| A、M=P |
| B、(∁UM)∩P=∅ |
| C、P⊆M |
| D、M⊆P |
函数f(x)是定义域为{x|x≠0}的奇函数,且f(1)=1,f′(x)为f(x)的导函数,当x>0时,f(x)+xf′(x)>
,则不等式xf(x)>1+ln|x|的解集为( )
| 1 |
| x |
| A、(-∞,-1)∪(1,+∞) |
| B、(-∞,-1) |
| C、(1,+∞) |
| D、(-1,1) |