题目内容
函数y=
-
的值域为 .
| x+1 |
| x-1 |
考点:函数的值域
专题:函数的性质及应用
分析:先把原函数整理成y=
判断出函数的单调性,进而求得函数的定义域,根据x的范围求得y的范围.
| 2 | ||||
|
解答:
解:y=
,
∵f(x)=
和函数f(x)=
均是单调递增函数,
∴y=
的单调性为单调减,
∵要使函数有意义需
,
∴x≥1,
∴ymax=
,
∵y=
-
>0,
∴函数的值域为(0,
],
故答案为:(0,
].
| 2 | ||||
|
∵f(x)=
| x+1 |
| x-1 |
∴y=
| 2 | ||||
|
∵要使函数有意义需
|
∴x≥1,
∴ymax=
| 2 |
∵y=
| x+1 |
| x-1 |
∴函数的值域为(0,
| 2 |
故答案为:(0,
| 2 |
点评:本题主要考查了函数的值域问题.对于带根号的函数,常利用分母有理化的形式对函数解析式变形.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
设a>0,b>0,若
是2a与b的等比中项,则
+
的最小值为( )
| 2 |
| 1 |
| a |
| 1 |
| b |
| A、2 | B、4 | C、8 | D、16 |
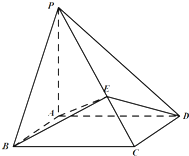 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为平行四边形,AB=1,BC=
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为平行四边形,AB=1,BC=