题目内容
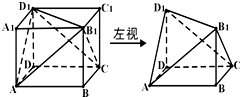
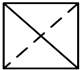
已知某个几何体是三视图（单位：cm）如图所示，则这个几何体的体积是 cm3．
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：利用三视图判断几何体的形状，通过三视图的数据求出几何体的体积即可．
解答：
解：三视图复原的几何体是圆锥；
底面半径为
，高为1.5，
几何体的体积为：
×(
)2π×
=
（cm3）．
故答案为：
．
底面半径为
| 1 |
| 2 |
几何体的体积为：
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
| π |
| 8 |
故答案为：
| π |
| 8 |
点评：本题考查简单几何体的三视图，三视图与几何体的对应关系，正确判断几何体的形状是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在极坐标系中，过点（2，
）且垂直于极轴的直线方程为（ ）
| π |
| 3 |
| A、ρsinθ=-1 |
| B、ρsinθ=1 |
| C、ρcosθ=-1 |
| D、ρcosθ=1 |
设a＞0，b＞0，若
是2a与b的等比中项，则
+
的最小值为（ ）
| 2 |
| 1 |
| a |
| 1 |
| b |
| A、2 | B、4 | C、8 | D、16 |
