题目内容
已知xy=1，则（xn+y6-n）8（n∈N*，n＜6）展开式的常数项为 ．
考点：二项式定理的应用
专题：二项式定理
分析：求得二项展开式的通项公式，要使该项为常数项，则有n（8-r）=r（6-n），可得n=3，r=4，从而求得常数项的值．
解答：
解：已知xy=1，则（xn+y6-n）8（n∈N*，n＜6）展开式的通项公式为 Tr+1=
•xn（8-r）•yr（6-n），
要使该项为常数项，则有n（8-r）=r（6-n），即4n=3r，再结合n∈N*，n＜6，可得n=3，r=4，
故展开式的常数项为
=70，
故答案为：70．
| C | r 8 |
要使该项为常数项，则有n（8-r）=r（6-n），即4n=3r，再结合n∈N*，n＜6，可得n=3，r=4，
故展开式的常数项为
| C | 4 8 |
故答案为：70．
点评：本题主要考查二项式定理的应用，二项展开式的通项公式，求展开式中某项的系数，属于基础题．
练习册系列答案
走进文言文系列答案
相关题目
已知集合P={y|y=-x2+2，x∈R}，Q={y|y=x，x∈R}，则P∩Q=（ ）
| A、R |
| B、{y|y≤2} |
| C、{y|y≥2} |
| D、{y|y＞2} |
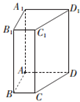已知四棱柱ABCD-A1B1C1D1，侧棱AA1⊥底面ABCD，底面ABCD中，AB⊥AD，BC∥AD，AB=2，AD=4，侧棱AA1=4．