题目内容
一张形状为正△ABC的纸片，边长为8，将它对折，使顶点A落在边BC上，求折痕长的最大值和最小值．
考点：两点间距离公式的应用
专题：解三角形
分析：直接由题意得到A点落在BC的中点上时，折痕最小，由三角形的中位线等于边长的一半求最小值，当A点与B（或C）重合时，此时折痕长最大，然后直接由勾股定理得答案．
解答：
解：由题意可知，当A点落在BC的中点上时，折痕最小，此时折痕长为边长的一半等于4．
当A点与B（或C）重合时，此时折痕长最大，最大值为
=4
．
∴折痕长的最大值和最小值分别为4
和4．
当A点与B（或C）重合时，此时折痕长最大，最大值为
| 82-42 |
| 3 |
∴折痕长的最大值和最小值分别为4
| 3 |
点评：本题考查了平面上两点间的距离，关键是明确折痕取得最大值和最小值的情况，是基础题．
练习册系列答案
相关题目
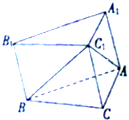如图，在斜三棱柱ABC-A1B1C1的底面△ABC中，∠BAC=90°，且BC1⊥AC，过C1作C1H⊥底面ABC，垂足为H，则点H在（ ）| A、直线AC上 |
| B、直线AB上 |
| C、直线BC上 |
| D、△ABC内部 |
设点（x0，0）在函数f（x）=sin（x-
）-1的图象上，其中
＜x0＜
，则cos（x0-
）的值为（ ）
| π |
| 3 |
| π |
| 2 |
| 4π |
| 3 |
| π |
| 6 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
如图所示，在△ABC中，