题目内容
设函数f（x）=2sin（
x+
）（-2＜x＜10）的图象与x轴交于点A，过点A的直线l与函数f（x）的图象交于另外两点B，C．O是坐标原点，则（
+
•
= ．
| π |
| 6 |
| π |
| 3 |
| OB |
| OC) |
| OA |
考点：两角和与差的正弦函数
专题：常规题型,三角函数的图像与性质,平面向量及应用
分析：先画出函数f（x）=2sin（
x+
）在-2＜x＜10上的图象，通过图象分析出点A是B、C的中点，然后根据向量的运算法则进行运算．
| π |
| 6 |
| π |
| 3 |
解答：
解：做出函数f（x）=2sin（
x+
）在-2＜x＜10上的图象如图：
由图象可知：图象关于点A对称，所以点A是点B与点C的中点
∴
+
=2
∴（
+
•
=2|
|2=2×42=32．
故答案为32．
| π |
| 6 |
| π |
| 3 |
由图象可知：图象关于点A对称，所以点A是点B与点C的中点
∴
| OB |
| OC |
| OA |
∴（
| OB |
| OC) |
| OA |
| OA |
故答案为32．
点评：本题考查了三角函数的图象与性质及向量的运算，解题的关键是通过画图分析出A点是B、C的中点．
练习册系列答案
相关题目
设点（x0，0）在函数f（x）=sin（x-
）-1的图象上，其中
＜x0＜
，则cos（x0-
）的值为（ ）
| π |
| 3 |
| π |
| 2 |
| 4π |
| 3 |
| π |
| 6 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
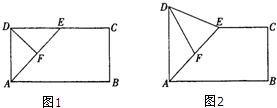如图所示，在长方形ABCD中，AB=2BC，E为CD的中点，F为AE的中点，现在沿AE将△ADE向上折起．