题目内容
设a∈R,x∈[-1,1]时,函数y=-x2-ax+b有最小值-1,最大值1,求使函数取得最小值和最大值时相应的x值.
考点:二次函数在闭区间上的最值
专题:函数的性质及应用
分析:首先把二次函数转化为顶点式,然后根据不定对称轴和单调区间的关系分五种情况进行讨论①当-
=0时②当0<-
<1时③当-1<-
<0时④当-
≥1时⑤当-
≤-1时,最后确定结果.
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
解答:
解:函数y=-x2-ax+b=-(x+
)2+
+b
则函数为开口方向线下,对称轴为x=-
的抛物线
当①-
=0时,即a=0
ymax=b=1 ymin=-1+a+b=-1
解得a=-1与a=0矛盾舍去
②当0<-
<1时,即0>a>-2时,ymax=
+b=1 ymin=-1+a+b=-1
解得:a=2±2
由于0>a>-2
所以a=2-2
③当-1<-
<0时,即0<a<2
ymax=
+b ymin=-1-a+b=-1
解得:a=-2±2
由于0<a<2
所以a=2
-2
④当-
≥1时,即a≤-2
函数在定义域内单调递增
ymax=-1-a+b=1 ymin=-1+a+b=1
解得:a=-1与a≤-2矛盾故舍去
⑤当-
≤-1时,即a≥2
函数在定义域内单调递减
ymax=-1+a+b=1 ymin=-1-a+b=1
解得:a=1与a≥2矛盾故舍去
综上所述:a=2-2
或a=2
-2
故答案为:a=2-2
或a=2
-2
| a |
| 2 |
| a2 |
| 4 |
则函数为开口方向线下,对称轴为x=-
| a |
| 2 |
当①-
| a |
| 2 |
ymax=b=1 ymin=-1+a+b=-1
解得a=-1与a=0矛盾舍去
②当0<-
| a |
| 2 |
| a2 |
| 4 |
解得:a=2±2
| 2 |
所以a=2-2
| 2 |
③当-1<-
| a |
| 2 |
ymax=
| a2 |
| 4 |
解得:a=-2±2
| 2 |
所以a=2
| 2 |
④当-
| a |
| 2 |
函数在定义域内单调递增
ymax=-1-a+b=1 ymin=-1+a+b=1
解得:a=-1与a≤-2矛盾故舍去
⑤当-
| a |
| 2 |
函数在定义域内单调递减
ymax=-1+a+b=1 ymin=-1-a+b=1
解得:a=1与a≥2矛盾故舍去
综上所述:a=2-2
| 2 |
| 2 |
故答案为:a=2-2
| 2 |
| 2 |
点评:本题考查的知识要点:二次函数顶点式与一般式的互化,不定对称轴和定区间的关系,及相关的分类讨论问题和运算问题

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
已知集合M={0,2,4},则下列各式中正确的是( )
| A、{0}∈M | B、2⊆M |
| C、{2,4}⊆M | D、Φ∈M |
数列{an}的前n项和为Sn,且Sn=2Sn+1+an2,a2=-1,则数列{an}的首项为( )
| A、1或-2 | B、±1 |
| C、±2 | D、-1或2 |
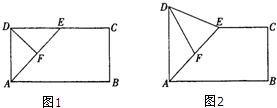 如图所示,在长方形ABCD中,AB=2BC,E为CD的中点,F为AE的中点,现在沿AE将△ADE向上折起.
如图所示,在长方形ABCD中,AB=2BC,E为CD的中点,F为AE的中点,现在沿AE将△ADE向上折起.