题目内容
已知集合P={y|y=-x2+2，x∈R}，Q={y|y=x，x∈R}，则P∩Q=（ ）
| A、R |
| B、{y|y≤2} |
| C、{y|y≥2} |
| D、{y|y＞2} |
考点：交集及其运算
专题：集合
分析：求出P与Q中y的范围确定出P与Q，找出两集合的交集即可．
解答：
解：由P中y=-x2+2≤2，得到P={y|y≤2}；由Q中y=x，得到Q=R，
则P∩Q={y|y≤2}．
故选：B．
则P∩Q={y|y≤2}．
故选：B．
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
已知集合M={0，2，4}，则下列各式中正确的是（ ）
| A、{0}∈M | B、2⊆M |
| C、{2，4}⊆M | D、Φ∈M |
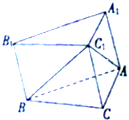如图，在斜三棱柱ABC-A1B1C1的底面△ABC中，∠BAC=90°，且BC1⊥AC，过C1作C1H⊥底面ABC，垂足为H，则点H在（ ）| A、直线AC上 |
| B、直线AB上 |
| C、直线BC上 |
| D、△ABC内部 |
设点（x0，0）在函数f（x）=sin（x-
）-1的图象上，其中
＜x0＜
，则cos（x0-
）的值为（ ）
| π |
| 3 |
| π |
| 2 |
| 4π |
| 3 |
| π |
| 6 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
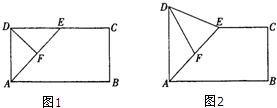如图所示，在长方形ABCD中，AB=2BC，E为CD的中点，F为AE的中点，现在沿AE将△ADE向上折起．