题目内容
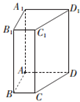 已知四棱柱ABCD-A1B1C1D1,侧棱AA1⊥底面ABCD,底面ABCD中,AB⊥AD,BC∥AD,AB=2,AD=4,侧棱AA1=4.
已知四棱柱ABCD-A1B1C1D1,侧棱AA1⊥底面ABCD,底面ABCD中,AB⊥AD,BC∥AD,AB=2,AD=4,侧棱AA1=4.(1)若E是AA1上一点,试确定E点位置使EB∥平面A1CD;
(2)在(1)的条件下,求平面BED与平面ABD所成角的余弦值.
考点:用空间向量求平面间的夹角,直线与平面平行的判定
专题:计算题,空间位置关系与距离,空间角
分析:(1)当E为AA1四等分点时,即A1E=
AA1时,EB∥平面A1CD.建立空间直角坐标系,确定E点坐标,即可得出结论;
(2)求出平面BED法向量、平面ABCD法向量,利用向量的夹角公式,即可求平面BED与平面ABD所成角的余弦值.
| 1 |
| 4 |
(2)求出平面BED法向量、平面ABCD法向量,利用向量的夹角公式,即可求平面BED与平面ABD所成角的余弦值.
解答:
解:(1)当E为AA1四等分点时,即A1E=
AA1时,EB∥平面A1CD.
证明:以AB为x轴,以AD为y轴,AA1为z轴建立空间直角坐标系,
因此A(0,0,0),B(2,0,0),D(0,4,0),C(2,1,0),A1(0,0,4),
设E(0,0,z),则
=(-2,0,z),
=(-2,-1,4),
=(-2,3,0).
∵EB∥平面A1CD,不妨设
=x
+y
,
∴(-2,0,z)=x(-2,-1,4)+y(-2,3,0).
∴
解得z=3.
所以当E点坐标为(0,0,3)即E为AA1且靠近A1的四等分点时,
EB∥平面A1CD.(6分)
(2)∵AA1⊥平面ABCD,
∴可设平面ABCD法向量为
=(0,0,1).
设平面BED法向量为
=(x,y,1),根据
=(-2,0,3),
=(-2,4,0),
∴
,
解得
=(
,
,1).
∴cos<
,
>=
=
.
由题意可得,平面BED与平面ABD所成角的余弦值为
.(12分)
| 1 |
| 4 |
证明:以AB为x轴,以AD为y轴,AA1为z轴建立空间直角坐标系,
因此A(0,0,0),B(2,0,0),D(0,4,0),C(2,1,0),A1(0,0,4),
设E(0,0,z),则
| BE |
| CA1 |
| CD |
∵EB∥平面A1CD,不妨设
| BE |
| CA1 |
| CD |
∴(-2,0,z)=x(-2,-1,4)+y(-2,3,0).
∴
|
所以当E点坐标为(0,0,3)即E为AA1且靠近A1的四等分点时,
EB∥平面A1CD.(6分)
(2)∵AA1⊥平面ABCD,
∴可设平面ABCD法向量为
| m |
设平面BED法向量为
| n |
| BE |
| BD |
∴
|
解得
| n |
| 3 |
| 2 |
| 3 |
| 4 |
∴cos<
| m |
| n |
| ||||
|
|
| 4 |
| 61 |
| 61 |
由题意可得,平面BED与平面ABD所成角的余弦值为
| 4 |
| 61 |
| 61 |
点评:本题考查线面平行,考查平面BED与平面ABD所成角的余弦值,建立空间直角坐标系,求出平面的法向量是关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
数列{an}的前n项和为Sn,且Sn=2Sn+1+an2,a2=-1,则数列{an}的首项为( )
| A、1或-2 | B、±1 |
| C、±2 | D、-1或2 |
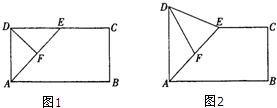 如图所示,在长方形ABCD中,AB=2BC,E为CD的中点,F为AE的中点,现在沿AE将△ADE向上折起.
如图所示,在长方形ABCD中,AB=2BC,E为CD的中点,F为AE的中点,现在沿AE将△ADE向上折起.