题目内容
f(x)是定义在R上的函数,且满足f(x+y)=f(x)+f(y)+2015成立,若函数g(x)=f(x)+sin2015x有最大值M和最小值m,则M+m= .
考点:抽象函数及其应用
专题:函数的性质及应用
分析:根据函数f(x)的特征,构造与f(x)、g(x)相关的奇函数,利用奇函数的图象对称性,得到相应的最值关系,从而得到g(x)的最大值M与最小值m的和,得到本题结论.
解答:
解:∵f(x)是定义在R上的函数,且对任意x,y∈R,均有f(x+y)=f(x)+f(y)+2015成立,
∴取x=y=0,得:f(0)=f(0)+f(0)+2015,f(0)=-2015,
取y=-x,得到:f(0)=f(x)+f(-x)+2015,
∴f(x)+f(-x)=-4030.
记h(x)=f(x)+sin2015x+2015,
则h(-x)+h(x)=[f(-x)+sin(-x)+2015]+f(x)+sin2015x+2015
=f(x)+f(-x)+4030=-4030+4030=0,
故y=h(x)为奇函数.
记h(x)的最大值为A,则最小值为-A.
∴g(x)=f(x)+sin2015x有最大值M=A-2015和最小值m=-A-2015,
则M+m=A-2015+(-A-2015)=-4030,
故答案为:-4030.
∴取x=y=0,得:f(0)=f(0)+f(0)+2015,f(0)=-2015,
取y=-x,得到:f(0)=f(x)+f(-x)+2015,
∴f(x)+f(-x)=-4030.
记h(x)=f(x)+sin2015x+2015,
则h(-x)+h(x)=[f(-x)+sin(-x)+2015]+f(x)+sin2015x+2015
=f(x)+f(-x)+4030=-4030+4030=0,
故y=h(x)为奇函数.
记h(x)的最大值为A,则最小值为-A.
∴g(x)=f(x)+sin2015x有最大值M=A-2015和最小值m=-A-2015,
则M+m=A-2015+(-A-2015)=-4030,
故答案为:-4030.
点评:本题考查了函数奇偶性及其应用,还考查了抽象函数和构造法,根据条件构造奇函数是解决本题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
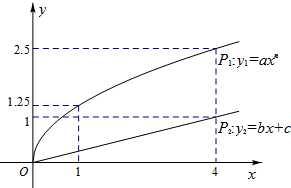 某企业拟用10万元投资甲、乙两种商品.已知各投入x万元,甲、乙两种商品可分别获得y1,y2万元的利润,利润曲线P1,P2如图所示.问怎样分配投资额,才能使投资获得最大利润?
某企业拟用10万元投资甲、乙两种商品.已知各投入x万元,甲、乙两种商品可分别获得y1,y2万元的利润,利润曲线P1,P2如图所示.问怎样分配投资额,才能使投资获得最大利润?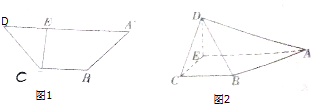 如图1,在等腰梯形ABCD中,AD∥BC,AD=3BC,CD=
如图1,在等腰梯形ABCD中,AD∥BC,AD=3BC,CD=