题目内容
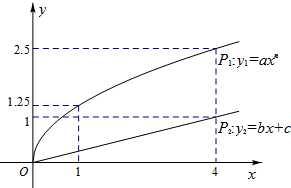 某企业拟用10万元投资甲、乙两种商品.已知各投入x万元,甲、乙两种商品可分别获得y1,y2万元的利润,利润曲线P1,P2如图所示.问怎样分配投资额,才能使投资获得最大利润?
某企业拟用10万元投资甲、乙两种商品.已知各投入x万元,甲、乙两种商品可分别获得y1,y2万元的利润,利润曲线P1,P2如图所示.问怎样分配投资额,才能使投资获得最大利润?考点:函数模型的选择与应用
专题:应用题,函数的性质及应用
分析:根据函数的模型求出两个函数解析式.将企业获利表示成对产品乙投资x的函数,再利用配方法,求出对称轴,即可求出函数的最值.
解答:
解:由图可得y1=
,(x≥0),y2=
x,(x≥0),
设用x万元投资甲商品,那么投资乙商品为(10-x)万元,总利润为y万元.y=
+
(10-x)=-
x+
+
=-
(
-
)2+
,(0≤x≤10)
当且仅当
=
即x=
=6.25时,ymax=
答:用6.25万元投资甲商品,3.75万元投资乙商品,才能获得最大利润.
(也可把投资乙商品设成x万元,把投资甲商品设成(10-x)万元)
| 5 |
| 4 |
| x |
| 1 |
| 4 |
设用x万元投资甲商品,那么投资乙商品为(10-x)万元,总利润为y万元.y=
| 5 |
| 4 |
| x |
| 1 |
| 4 |
| 1 |
| 4 |
| 5 |
| 4 |
| x |
| 10 |
| 4 |
| 1 |
| 4 |
| x |
| 5 |
| 2 |
| 65 |
| 16 |
当且仅当
| x |
| 5 |
| 2 |
| 25 |
| 4 |
| 65 |
| 16 |
答:用6.25万元投资甲商品,3.75万元投资乙商品,才能获得最大利润.
(也可把投资乙商品设成x万元,把投资甲商品设成(10-x)万元)
点评:本题考查将实际问题的最值问题转化为函数的最值问题、考查二次函数的最值,属于中档题.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
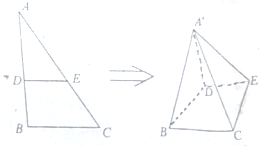 如图,在直角△ABC中,B=90°,BC=1,AB=
如图,在直角△ABC中,B=90°,BC=1,AB=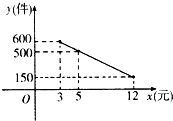 某商品经营部每天的房租、人员工资等固定成本为300元,已知该商品进价为3元/件,并规定其销售单价不低于商品进价,且不高于12元,该商品日均销售量y(件)与销售单价x(元)的关系如图所示.
某商品经营部每天的房租、人员工资等固定成本为300元,已知该商品进价为3元/件,并规定其销售单价不低于商品进价,且不高于12元,该商品日均销售量y(件)与销售单价x(元)的关系如图所示. 对某小区居民一个月内参加娱乐活动的次数进行统计,随机抽取M名居民作为样本,得到这M名居民参加娱乐活动的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如下:
对某小区居民一个月内参加娱乐活动的次数进行统计,随机抽取M名居民作为样本,得到这M名居民参加娱乐活动的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如下: