题目内容
已知函数f(x)=ax2-2x-1,(a∈R).
(1)讨论函数f(x)的单调性;
(2)解关于x的方程f(x)=0;
(3)当a≥1时,f(x)在[2,4]上的最小值为3,求f(x)在[2,4]上的最大值.
(1)讨论函数f(x)的单调性;
(2)解关于x的方程f(x)=0;
(3)当a≥1时,f(x)在[2,4]上的最小值为3,求f(x)在[2,4]上的最大值.
考点:函数的最值及其几何意义,二次函数的性质
专题:函数的性质及应用
分析:(1)讨论a,结合一元二次函数的性质即可判断函数f(x)的单调性;
(2)讨论a的取值范围即可解关于x的方程f(x)=0;
(3)当a≥1时,判断函数的单调性,结合函数f(x)的对称轴之间的关系即可得到结论.
(2)讨论a的取值范围即可解关于x的方程f(x)=0;
(3)当a≥1时,判断函数的单调性,结合函数f(x)的对称轴之间的关系即可得到结论.
解答:
解:(1)当a=0时,函数f(x)=-2x-1在R上为减函数;…(1分)
当a≠0时,f(x)的对称轴为x=
若a>0时,函数f(x)在(-∞,
]上为减函数,在[
,+∞)上为增函数 …(3分)
若a<0时,函数f(x)在(-∞,
]上为增函数,在[
,+∞)上为减函数 …(5分)
(2)方程f(x)=0,即ax2-2x-1=0
当a=0时,方程-2x-1=0有1个实根x=-
,…(6分)
当a≠0时,△=4+4a…(7分)
①若△<0,即a<-1时,方程ax2-2x-1=0没有实根 …(8分)
②若△=0,即a=-1时,方程ax2-2x-1=0有1个实根x=-1…(9分)
③若△>0,即a>-1且a≠0时,方程ax2-2x-1=0有2个实根x=
…(10分)
(3)当a≥1时,函数f(x)=ax2-2x-1开口向上,对称轴为x=
∈(0,1]…(11分)
∴f(x)在区间[2,4]上为增函数
∴f(x)min=f(2)=4a-5=3,得a=2
∴f(x)=2x2-2x-1…(13分)
∴f(x)max=f(4)=23…(14分)
当a≠0时,f(x)的对称轴为x=
| 1 |
| a |
若a>0时,函数f(x)在(-∞,
| 1 |
| a |
| 1 |
| a |
若a<0时,函数f(x)在(-∞,
| 1 |
| a |
| 1 |
| a |
(2)方程f(x)=0,即ax2-2x-1=0
当a=0时,方程-2x-1=0有1个实根x=-
| 1 |
| 2 |
当a≠0时,△=4+4a…(7分)
①若△<0,即a<-1时,方程ax2-2x-1=0没有实根 …(8分)
②若△=0,即a=-1时,方程ax2-2x-1=0有1个实根x=-1…(9分)
③若△>0,即a>-1且a≠0时,方程ax2-2x-1=0有2个实根x=
1±
| ||
| a |
(3)当a≥1时,函数f(x)=ax2-2x-1开口向上,对称轴为x=
| 1 |
| a |
∴f(x)在区间[2,4]上为增函数
∴f(x)min=f(2)=4a-5=3,得a=2
∴f(x)=2x2-2x-1…(13分)
∴f(x)max=f(4)=23…(14分)
点评:本题主要考查函数单调性和函数最值的求解,利用一元二次函数的性质结合一元二次函数对称性的性质是解决本题的关键.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
若直线y=a与函数y=sinx的图象相交,则相邻的两交点间的距离的最大值为( )
A、
| ||
| B、π | ||
C、
| ||
| D、2π |
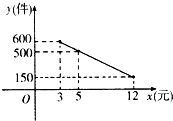 某商品经营部每天的房租、人员工资等固定成本为300元,已知该商品进价为3元/件,并规定其销售单价不低于商品进价,且不高于12元,该商品日均销售量y(件)与销售单价x(元)的关系如图所示.
某商品经营部每天的房租、人员工资等固定成本为300元,已知该商品进价为3元/件,并规定其销售单价不低于商品进价,且不高于12元,该商品日均销售量y(件)与销售单价x(元)的关系如图所示.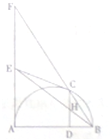 如图,EA,EC是以AB为直径的半圆的切线,AE与BC的延长线交于点F,过点C作CD⊥AB交AB于D,交BE于H.
如图,EA,EC是以AB为直径的半圆的切线,AE与BC的延长线交于点F,过点C作CD⊥AB交AB于D,交BE于H.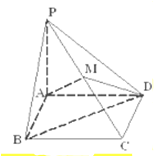 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥底面ABCD,
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥底面ABCD,