题目内容
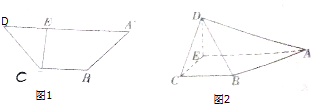 如图1,在等腰梯形ABCD中,AD∥BC,AD=3BC,CD=
如图1,在等腰梯形ABCD中,AD∥BC,AD=3BC,CD=| 2 |
(1)如果在AD上存在一点F,使BF∥平面DCE,证明:F为AD的中点;
(2)求二面角C-BD-A的大小.
考点:二面角的平面角及求法,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)由已知得AE=2BC,取AD中点F,AE中点M,连结FM、BF、BM,从而FM∥DE,BC
ME,进而四边形BCEM是平行四边形,BM∥EC,由此得到平面DEC∥平面FMB,从而BF∥平面DCE,进而能证明在AD上存在一点F,使BF∥平面DCE,则F为AD的中点.
(2)以E为原点,EC为x轴,EA为y轴,ED为z轴,建立空间直角坐标系,设BC=1,求出平面BDC的法向量和平面ABD的法向量,由此利用向量法能求出二面角C-BD-A的大小.
| ∥ |
. |
(2)以E为原点,EC为x轴,EA为y轴,ED为z轴,建立空间直角坐标系,设BC=1,求出平面BDC的法向量和平面ABD的法向量,由此利用向量法能求出二面角C-BD-A的大小.
解答:
(1)证明: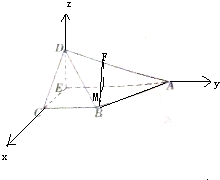 ∵在等腰梯形ABCD中,AD∥BC,AD=3BC,
∵在等腰梯形ABCD中,AD∥BC,AD=3BC,
过C作CE⊥AD于E,
∴AE=2BC,取AD中点F,AE中点M,连结FM、BF、BM,
则FM∥DE,BC
ME,∴四边形BCEM是平行四边形,
∴BM∥EC,又BM∩FM=M,
∴平面DEC∥平面FMB,
又BF?平面BMF,∴BF∥平面DCE,
故在AD上存在一点F,使BF∥平面DCE,则F为AD的中点.
(2)解:∵CE⊥AD于E,沿CE折叠,使平面DCE⊥平面ABCE,
∴EC、EA、ED两两垂直,以E为原点,EC为x轴,EA为y轴,ED为z轴,
建立空间直角坐标系,设BC=1,
则C(1,0,0),B(1,1,0),D(0,0,1),A(0,2,0),
=(-1,-1,1),
=(0,-1,0),
=(-1,1,0),
设平面BDC的法向量
=(x,y,z),
则
,取x=1,得
=(1,0,1),
设平面ABD的法向量
=(a,b,c),
则
,取a=1,得
=(1,1,2),
设二面角C-BD-A的平面角为θ,
cosθ=
=
=
,∴θ=
.
∴二面角C-BD-A的大小为
.
 ∵在等腰梯形ABCD中,AD∥BC,AD=3BC,
∵在等腰梯形ABCD中,AD∥BC,AD=3BC,过C作CE⊥AD于E,
∴AE=2BC,取AD中点F,AE中点M,连结FM、BF、BM,
则FM∥DE,BC
| ∥ |
. |
∴BM∥EC,又BM∩FM=M,
∴平面DEC∥平面FMB,
又BF?平面BMF,∴BF∥平面DCE,
故在AD上存在一点F,使BF∥平面DCE,则F为AD的中点.
(2)解:∵CE⊥AD于E,沿CE折叠,使平面DCE⊥平面ABCE,
∴EC、EA、ED两两垂直,以E为原点,EC为x轴,EA为y轴,ED为z轴,
建立空间直角坐标系,设BC=1,
则C(1,0,0),B(1,1,0),D(0,0,1),A(0,2,0),
| BD |
| BC |
| BA |
设平面BDC的法向量
| n |
则
|
| n |
设平面ABD的法向量
| m |
则
|
| m |
设二面角C-BD-A的平面角为θ,
cosθ=
|
| ||||
|
|
| 3 | ||||
|
| ||
| 2 |
| π |
| 6 |
∴二面角C-BD-A的大小为
| π |
| 6 |
点评:本题主要考查直线与平面之间的平行、垂直等位置关系,线线角、线面角、二面角的概念、求法等知识,以及空间想象能力和逻辑推理能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数y=x•e-x在x∈[2,4]上的最小值为( )
| A、0 | ||
B、
| ||
C、
| ||
D、
|
 如图,在直角△ABC中,B=90°,BC=1,AB=
如图,在直角△ABC中,B=90°,BC=1,AB= 对某小区居民一个月内参加娱乐活动的次数进行统计,随机抽取M名居民作为样本,得到这M名居民参加娱乐活动的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如下:
对某小区居民一个月内参加娱乐活动的次数进行统计,随机抽取M名居民作为样本,得到这M名居民参加娱乐活动的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如下: 如图AC是圆O的直径,B、D是圆O上两点,AC=2BC=2CD=2,PA⊥圆O所在的平面,
如图AC是圆O的直径,B、D是圆O上两点,AC=2BC=2CD=2,PA⊥圆O所在的平面,