题目内容

已知矩阵A的逆矩阵A-1=
2
2
2
2
-
2
2
2
2
．
（Ⅰ）求矩阵A；
（Ⅱ）求曲线xy=1在矩阵A所对应的线性变换作用下所得的曲线方程．
考点：逆变换与逆矩阵,几种特殊的矩阵变换,逆矩阵与投影变换
专题：矩阵和变换
分析：（Ⅰ）直接计算即可；
（Ⅱ）先设xy=1上任意一点（x，y）在矩阵A所对应的线性变换作用下的像为点（x′，y′），然后计算即可．
解答： 解：（Ⅰ）因为矩阵A是矩阵A-1的逆矩阵，
且
.
A-1
.
=
.
2
2
×
2
2
-
2
2
×(-
2
2
)
.
=1≠0，
所以A=
2
2
-
2
2
2
2
2
2
．
（Ⅱ）设xy=1上任意一点（x，y）在矩阵A所对应的线性变换作用下的像为点（x′，y′），
则
x
y
=A-1
x′
y′
=
2
2
2
2
-
2
2
2
2
x′
y′
，
由此得
x=
2
2
(x′+y′)
y=
2
2
(y′-x′)
，
代入方程xy=1，得y′2-x′2=2．
所以xy=1在矩阵A所对应的线性变换作用下的曲线方程为y2-x2=2．
点评：本小题主要考查矩阵及其逆矩阵、求曲线在矩阵所对应的线性变换作用下的曲线的方程等基础知识，考查运算求解能力，考查化归与转化思想．
练习册系列答案
相关题目
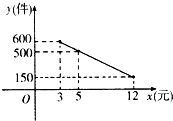已知△ABC的内角∠A、∠B、∠C所对的边分别为a、b、c，若∠A＞∠B＞∠C，∠A=2∠C，b=4，a+c=8，则a的值为
 
．
已知圆锥大径D=30mm，小径d=20mm，锥的长度l=40mm，求此圆锥的锥度比．
某商品经营部每天的房租、人员工资等固定成本为300元，已知该商品进价为3元/件，并规定其销售单价不低于商品进价，且不高于12元，该商品日均销售量y（件）与销售单价x（元）的关系如图所示．
（1）试求y关于x的函数解析式；
（2）当销售单价定为多少元时，该商品每天的利润最大？
对某小区居民一个月内参加娱乐活动的次数进行统计，随机抽取M名居民作为样本，得到这M名居民参加娱乐活动的次数，根据此数据作出了频数与频率的统计表和频率分布直方图如下：
（I）求出表中的M，p及图中a的值；
（Ⅱ）试估计这M名居民在一个月内参加娱乐活动的平均次数（同一组的数据用该组的中间值作代表）；
（Ⅲ）在所取样本中，从参加娱乐活动次数不少于20次的居民中任取2人，求两人参加娱乐活动次数都在区间[20，25）内的概率．
分组频数频率
[10，15）100.25
[15，20）24n
[20，25）mp
[25，30）10.05
合计M1
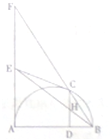如图，EA，EC是以AB为直径的半圆的切线，AE与BC的延长线交于点F，过点C作CD⊥AB交AB于D，交BE于H．
（1）证明：E是AF的中点；
（2）若∠F=30°，AB=2，求CH的长度．
f（x）是定义在R上的函数，且满足f（x+y）=f（x）+f（y）+2015成立，若函数g（x）=f（x）+sin2015x有最大值M和最小值m，则M+m=
 
．
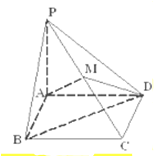如图，在四棱锥P-ABCD中，底面ABCD是边长为1的正方形，PA⊥底面ABCD，
点M是棱PC的中点，AM⊥平面PBD
（1）求四棱锥P-ABCD的体积；
（2）求平面PAD与平面AMD所成二面角的大小．
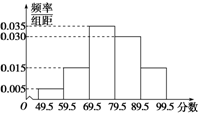某校在“创新素质实践行”活动中组织学生进行社会调查，并对学生的调查报告进行了评比．如图所示的是将某年级60篇学生调查报告进行整理，分成5组画出的频率分布直方图．那么在这次评比中被评为优秀的调查报告有（分数大于或等于80分为优秀且分数为整数）（　　）
A、18篇B、24篇
C、25篇D、27篇

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网