题目内容
已知f(x)对任意的实数m,n都有:f(m+n)=f(m)+f(n)-1,且当x>0时,有f(x)>1.
(1)求f(0);
(2)求证:f(x)在R上为增函数;
(3)若f(1)=2,且关于x的不等式f(ax-2)+f(x-x2)<3对任意的x∈[1,+∞)恒成立,求实数a的取值范围.
(1)求f(0);
(2)求证:f(x)在R上为增函数;
(3)若f(1)=2,且关于x的不等式f(ax-2)+f(x-x2)<3对任意的x∈[1,+∞)恒成立,求实数a的取值范围.
考点:函数恒成立问题,函数单调性的判断与证明,抽象函数及其应用
专题:函数的性质及应用
分析:(1)令m=0即可;
(2)根据函数单调性的定义进行证明,将f(x2)变形成f[(x2-x1)+x1]=f(x2-x1)+f(x1)-1>1+f(x1)-1=f(x1),从而得到函数的单调性;
(3)f(ax-2)+f(x-x2)=f(ax-2+x-x2)+1<3,根据f(1)=2及f(x)在R上为增函数即得x2-(a+1)x+3>0对任意的x∈[1,+∞)恒成立,故只需讨论△的正负情况即可.
(2)根据函数单调性的定义进行证明,将f(x2)变形成f[(x2-x1)+x1]=f(x2-x1)+f(x1)-1>1+f(x1)-1=f(x1),从而得到函数的单调性;
(3)f(ax-2)+f(x-x2)=f(ax-2+x-x2)+1<3,根据f(1)=2及f(x)在R上为增函数即得x2-(a+1)x+3>0对任意的x∈[1,+∞)恒成立,故只需讨论△的正负情况即可.
解答:
(1)解:令m=0,则f(0+n)=f(0)+f(n)-1,即f(0)=1;
(2)证明:任取x1,x2∈R且x1<x2,则x2-x1>0,
∵当x>0时,有f(x)>1,
∴f(x2-x1)>1,
∵f(x2)=f[(x2-x1)+x1]=f(x2-x1)+f(x1)-1>1+f(x1)-1=f(x1),
∴f(x2)>f(x1),
即f(x)在R上为增函数;
(3)∵f(ax-2)+f(x-x2)=f(ax-2+x-x2)+1<3
∴f(ax-2+x-x2)<2
又∵f(1)=2及f(x)在R上为增函数
∴ax-2+x-x2<1对任意的x∈[1,+∞)恒成立,
即x2-(a+1)x+3>0对任意的x∈[1,+∞)恒成立.
下面对△=(a+1)2-12的正负情况进行讨论:
①当△<0,即(a+1)2-12<0时,
-2
-1<a<2
-1
②当△=0且x2-(a+1)x+3=0的解小于1时,
则a=±2
-1,x=
<1,
故a=-2
-1;
③当△>0且x2-(a+1)x+3=0的最大解小于1时,
即0<a2+2a-11<a2-2a+1,
解得a<-2
-1或2
-1<a<3,
综合所述,a<2
-1或2
-1<a<3.
(2)证明:任取x1,x2∈R且x1<x2,则x2-x1>0,
∵当x>0时,有f(x)>1,
∴f(x2-x1)>1,
∵f(x2)=f[(x2-x1)+x1]=f(x2-x1)+f(x1)-1>1+f(x1)-1=f(x1),
∴f(x2)>f(x1),
即f(x)在R上为增函数;
(3)∵f(ax-2)+f(x-x2)=f(ax-2+x-x2)+1<3
∴f(ax-2+x-x2)<2
又∵f(1)=2及f(x)在R上为增函数
∴ax-2+x-x2<1对任意的x∈[1,+∞)恒成立,
即x2-(a+1)x+3>0对任意的x∈[1,+∞)恒成立.
下面对△=(a+1)2-12的正负情况进行讨论:
①当△<0,即(a+1)2-12<0时,
-2
| 3 |
| 3 |
②当△=0且x2-(a+1)x+3=0的解小于1时,
则a=±2
| 3 |
| a+1 |
| 2 |
故a=-2
| 3 |
③当△>0且x2-(a+1)x+3=0的最大解小于1时,
即0<a2+2a-11<a2-2a+1,
解得a<-2
| 3 |
| 3 |
综合所述,a<2
| 3 |
| 3 |
点评:本题主要考查了抽象函数,及其函数的单调性和不等式的解法,着重考查了函数的简单性质和函数恒成立问题等知识点,属于中档题.

练习册系列答案
相关题目
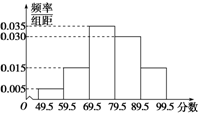 某校在“创新素质实践行”活动中组织学生进行社会调查,并对学生的调查报告进行了评比.如图所示的是将某年级60篇学生调查报告进行整理,分成5组画出的频率分布直方图.那么在这次评比中被评为优秀的调查报告有(分数大于或等于80分为优秀且分数为整数)( )
某校在“创新素质实践行”活动中组织学生进行社会调查,并对学生的调查报告进行了评比.如图所示的是将某年级60篇学生调查报告进行整理,分成5组画出的频率分布直方图.那么在这次评比中被评为优秀的调查报告有(分数大于或等于80分为优秀且分数为整数)( )| A、18篇 | B、24篇 |
| C、25篇 | D、27篇 |
函数y=x•e-x在x∈[2,4]上的最小值为( )
| A、0 | ||
B、
| ||
C、
| ||
D、
|
 如图,节日花坛中有5个区域,要把4种不同颜色的花分别种植到这5个区域中,要求相同颜色的花不能相邻栽种,一共有多少种种植方案?
如图,节日花坛中有5个区域,要把4种不同颜色的花分别种植到这5个区域中,要求相同颜色的花不能相邻栽种,一共有多少种种植方案?