题目内容
已知数列{an}、{bn}的各项均为正数且对任意n∈N+,都有an,bn,an+1成等差数列,bn,an+1,bn+1成等比数列,且a1=10,a2=15.
(1)求证:数列{
}是等差数列并求出数列{an}、{bn}的通项公式;
(2)设Sn=
+
+…+
,如果对任意n∈N+,不等式2a•Sn<2-
恒成立,求实数a的取值范围.
(1)求证:数列{
| bn |
(2)设Sn=
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| bn |
| an |
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(1)由已知得2bn=an+an+1,an+12=bnbn+1,进一步得an+1=
,联立后可得{
}是等差数列,由等差数列的通项公式求数列{
}的通项公式,进一步求得{bn}的通项公式,结合an=
求得数列{an}的通项公式;
(2)由(1)得
=
,然后利用裂项相消法求得Sn,代入不等式2aSn<2-
化为4a(
-
)<2-
,然后转化为关于n的函数分类求解实数a的取值范围.
| bnbn+1 |
| bn |
| bn |
| bn-1bn |
(2)由(1)得
| 1 |
| an |
| 2 |
| (n+3)(n+4) |
| bn |
| an |
| 1 |
| 4 |
| 1 |
| n+4 |
| n+4 |
| n+3 |
解答:
(1)证明:由已知,得2bn=an+an+1 ①,
an+12=bnbn+1 ②,
由②可得an+1=
③,
将③代入①,得对任意n≥2,n∈N*,有2bn=
+
,即2
=
+
,
∴{
}是等差数列.
设数列{
}的公差为d,由a1=10,a2=15,得b1=
,b2=18,
∴
=
,
=3
,d=
-
=
,
∴
=
+(n-1)d=
+
(n-1)=
(n+4),bn=
.
由已知,当n≥2时,an=
=
,而a1=10也满足此式.
∴数列{an}、{bn}的通项公式为:an=
,bn=
.
(2)解:由(1),得
=
=2(
-
),
则Sn=2[(
-
)+(
-
)+…+(
-
)]=2(
-
)=2(
-
),
不等式2aSn<2-
化为4a(
-
)<2-
,
不等式化为(a-1)n2+(3a-6)n-8<0,
设f(n)=(a-1)n2+(3a-6)n-8,则f(n)<0对任意n∈N*恒成立.
当a-1>0,即a>1时,不满足条件.
当a-1=0,即a=1时,满足条件.
当a-1<0,即a<1时,函数f(n)图象的对称轴为直线x=-
<0,f(n)关于n递减,
只需f(1)=4a-15<0,解得a<
,故a<1.
综上可得,a的取值范围是(-∞,1].
an+12=bnbn+1 ②,
由②可得an+1=
| bnbn+1 |
将③代入①,得对任意n≥2,n∈N*,有2bn=
| bn-1bn |
| bnbn+1 |
| bn |
| bn-1 |
| bn |
∴{
| bn |
设数列{
| bn |
| 25 |
| 2 |
∴
| b1 |
5
| ||
| 2 |
| b2 |
| 2 |
| b2 |
| b1 |
| ||
| 2 |
∴
| bn |
| b1 |
5
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| (n+4)2 |
| 2 |
由已知,当n≥2时,an=
| bn-1bn |
| (n+3)(n+4) |
| 2 |
∴数列{an}、{bn}的通项公式为:an=
| (n+3)(n+4) |
| 2 |
| (n+4)2 |
| 2 |
(2)解:由(1),得
| 1 |
| an |
| 2 |
| (n+3)(n+4) |
| 1 |
| n+3 |
| 1 |
| n+4 |
则Sn=2[(
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| n+3 |
| 1 |
| n+4 |
| 1 |
| 4 |
| 1 |
| n+4 |
| 1 |
| 4 |
| 1 |
| n+4 |
不等式2aSn<2-
| bn |
| an |
| 1 |
| 4 |
| 1 |
| n+4 |
| n+4 |
| n+3 |
不等式化为(a-1)n2+(3a-6)n-8<0,
设f(n)=(a-1)n2+(3a-6)n-8,则f(n)<0对任意n∈N*恒成立.
当a-1>0,即a>1时,不满足条件.
当a-1=0,即a=1时,满足条件.
当a-1<0,即a<1时,函数f(n)图象的对称轴为直线x=-
| 3(a-2) |
| 2(a-1) |
只需f(1)=4a-15<0,解得a<
| 15 |
| 4 |
综上可得,a的取值范围是(-∞,1].
点评:本题考查了等差数列和等比数列的性质,考查了裂项相消法求数列的前n项和,考查了数学转化、分类讨论等数学思想方法,考查了数列的函数特性,是中档题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积为( )


| A、12+π | B、8+π |
| C、12-π | D、6-π |
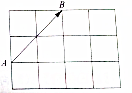 如图所示是4×3的矩形(每个小方格都是单位正方形),在起点和中点都在小方格的顶点处的向量中,试问:
如图所示是4×3的矩形(每个小方格都是单位正方形),在起点和中点都在小方格的顶点处的向量中,试问: