题目内容
已知函数f(x)=2
sinωxcosωx+cos2ωx-sin2ωx,其中ω>0,x∈R,若函数f(x)的最小正周期为π.
(1)求ω的值;
(2)在△ABC中,若f(B)=-2,BC=
,sinB=
sinA,求
•
的值.
| 3 |
(1)求ω的值;
(2)在△ABC中,若f(B)=-2,BC=
| 3 |
| 3 |
| BA |
| BC |
考点:三角函数中的恒等变换应用,平面向量数量积的运算
专题:解三角形
分析:(1)利用三角函数中的恒等变换应用化简函数解析式可得f(x)=2sin(2ωx+
),利用函数f(x)的最小正周期为π,ω>0,可得
=π,解得ω即可.
(2)由(1)可得:f(x)=2sin(2x+
).由f(B)=-2,可得sin(2B+
)=-1,结合B∈(0,π)可求B=
.利用BC=
,sinB=
sinA,可得a=
,b=
a.由正弦定理可得:
=
,解得sinA,C,c.再利用数量积运算性质即可得解.
| π |
| 6 |
| 2π |
| 2ω |
(2)由(1)可得:f(x)=2sin(2x+
| π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| ||
| sinA |
| 3 | ||
sin
|
解答:
解:(1)f(x)=2
sinωxcosωx+cos2ωx-sin2ωx
=
sin2ωx+cos2ωx
=2sin(2ωx+
)
∵函数f(x)的最小正周期为π,ω>0,
∴由周期公式可得:T=π=
,可解得:ω=1.
(2)由(1)可得:f(x)=2sin(2x+
).
∵f(B)=-2,∴2sin(2B+
)=-2,∴sin(2B+
)=-1,B∈(0,π).
∴B=
.
∵BC=
,sinB=
sinA,
∴a=
,b=
a.∴b=3.由正弦定理可得:
=
,解得sinA=
,
∵A∈(0,
),∴A=
.∴C=
,c=
.
∴
•
=cacosB=
×
cos
=-
.
| 3 |
=
| 3 |
=2sin(2ωx+
| π |
| 6 |
∵函数f(x)的最小正周期为π,ω>0,
∴由周期公式可得:T=π=
| 2π |
| 2ω |
(2)由(1)可得:f(x)=2sin(2x+
| π |
| 6 |
∵f(B)=-2,∴2sin(2B+
| π |
| 6 |
| π |
| 6 |
∴B=
| 2π |
| 3 |
∵BC=
| 3 |
| 3 |
∴a=
| 3 |
| 3 |
| ||
| sinA |
| 3 | ||
sin
|
| 1 |
| 2 |
∵A∈(0,
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 3 |
∴
| BA |
| BC |
| 3 |
| 3 |
| 2π |
| 3 |
| 3 |
| 2 |
点评:本题考查了数量积运算性质、倍角公式、两角和差的余弦公式、三角函数的图象与性质、正弦定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
等差数列{an}的公差d≠0,a1=20,且a3,a7,a9成等比数列.Sn为{an}的前n项和,则S10的值为( )
| A、-110 | B、-90 |
| C、90 | D、110 |
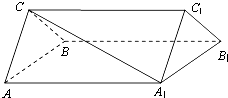 如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°,E为BC中点
如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°,E为BC中点