题目内容
设a>1,若关于x的方程ax=logax有实根,则a的取值范围为 .
考点:函数的零点与方程根的关系
专题:综合题,函数的性质及应用
分析:函数y=ax与y=logax关于y=x对称,只需要讨论与y=x有解即可,构造函数h(x)=ax-x,只须h(x)的最小值小于等于0,进而得到实数a的取值范围.
解答:
解:由于函数y=ax与y=logax关于y=x对称,只需要讨论与y=x有解即可,
令h(x)=ax-x,则函数h(x)有零点,
当a>1时,令h′(x)=axlna-1=0,则x=loga
,
当0<x<loga
时,h′(x)<0,此时函数h(x)为减函数;
当x>loga
时,h′(x)>0,此时函数h(x)为增函数;
故当x=loga
时,函数h(x)取最小值,
若函数h(x)有零点,则h(loga
)≤0,
即
=logae≤loga
,
即e≤
,
即0<lna≤
,
即1<a≤e
,
故实数a的取值范围是(1,e
],
故答案为:(1,e
].
令h(x)=ax-x,则函数h(x)有零点,
当a>1时,令h′(x)=axlna-1=0,则x=loga
| 1 |
| lna |
当0<x<loga
| 1 |
| lna |
当x>loga
| 1 |
| lna |
故当x=loga
| 1 |
| lna |
若函数h(x)有零点,则h(loga
| 1 |
| lna |
即
| 1 |
| lna |
| 1 |
| lna |
即e≤
| 1 |
| lna |
即0<lna≤
| 1 |
| e |
即1<a≤e
| 1 |
| e |
故实数a的取值范围是(1,e
| 1 |
| e |
故答案为:(1,e
| 1 |
| e |
点评:本题考查的知识点是根的存在性及根的个数判断,反函数,导数法判断函数的单调性,导数法求函数的最值,对数的运算性质,是指数函数,对数函数,函数零点,导数等的综合应用,运算量大,综合性可,转化困难,属于难题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
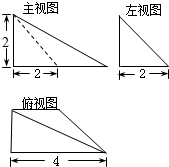 已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的体积是( )
已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的体积是( )| A、2 | B、4 | C、6 | D、12 |
