题目内容
销售甲、乙两种商品所得利润分别为P(单位:万元)和Q(单位:万元),它们与投入资金m(单位:万元)的关系有经验公式P=
m,P=
m,Q=
.今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投资x(单位:万元)
(1)试建立总利润y(单位:万元)关于x的函数关系式,并指明函数定义域;
(2)如何投资经营甲、乙两种商品,才能使得总利润最大.
| 1 |
| 5 |
| 1 |
| 5 |
| 3 |
| 5 |
| m |
(1)试建立总利润y(单位:万元)关于x的函数关系式,并指明函数定义域;
(2)如何投资经营甲、乙两种商品,才能使得总利润最大.
考点:函数模型的选择与应用
专题:应用题,函数的性质及应用
分析:(1)根据题意,对甲种商品投资x(万元),对乙种商品投资(3-x)(万元),利用经验公式P=
m,Q=
,可求经营甲、乙两种商品的总利润y(万元)关于x的函数表达式;
(2)利用配方法,可求总利润y的最大值.
| 1 |
| 5 |
| 3 |
| 5 |
| m |
(2)利用配方法,可求总利润y的最大值.
解答:
解:(1)根据题意,对甲种商品投资x(万元),对乙种商品投资(3-x)(万元).
所以y=
x+
-----------------------(4分)
其定义域为[0,3]-----------------------(6分)
(2)令t=
,
因为x∈[0,3],
所以t∈[0,
],有y=
x+
=-
t2+
t+
-------(10分)
=-
(t-
)2+
-----------------(12分)
所以当t=
∈[0,
]时,即x=
时,ymax=
--------------(14分)
答:当甲商品投入
万元,乙商品投入
万元时,总利润最大为
万元.---------(16分)
所以y=
| 1 |
| 5 |
| 3 |
| 5 |
| 3-x |
其定义域为[0,3]-----------------------(6分)
(2)令t=
| 3-x |
因为x∈[0,3],
所以t∈[0,
| 3 |
| 1 |
| 5 |
| 3 |
| 5 |
| 3-x |
| 1 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
=-
| 1 |
| 5 |
| 3 |
| 2 |
| 21 |
| 20 |
所以当t=
| 3 |
| 2 |
| 3 |
| 3 |
| 4 |
| 21 |
| 20 |
答:当甲商品投入
| 3 |
| 4 |
| 9 |
| 4 |
| 21 |
| 20 |
点评:本题考查利用数学知识解决实际问题,考查函数的最值,正确建立函数解析式是关键.

练习册系列答案
相关题目
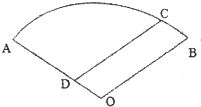 吉安一中新校区正在如火如荼地建设中,如图,某工地的平面图呈圆心角为120°的扇形AOB,工地的两个出入口设置在点A及点C处,工地中有两条笔直的小路AD、DC,长度分别为300米、500米,且DC平行于OB.求该扇形的半径OA的长(精确到1米).
吉安一中新校区正在如火如荼地建设中,如图,某工地的平面图呈圆心角为120°的扇形AOB,工地的两个出入口设置在点A及点C处,工地中有两条笔直的小路AD、DC,长度分别为300米、500米,且DC平行于OB.求该扇形的半径OA的长(精确到1米).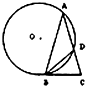 如图,△ABC中AB=AC,∠ABC=72°,圆O过A,B且与BC切于B点,与AC交于D点,连BD.若BC=2,则AC=
如图,△ABC中AB=AC,∠ABC=72°,圆O过A,B且与BC切于B点,与AC交于D点,连BD.若BC=2,则AC=