题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,且sin2A+sin2B+cos2C=1+sinAsinB
(1)求角C的大小;
(2)若c=2,且△ABC的面积为
,求a,b.
(1)求角C的大小;
(2)若c=2,且△ABC的面积为
| 3 |
考点:余弦定理,正弦定理
专题:计算题,解三角形
分析:(1)利用正弦定理化简已知的等式,得到三边的关系式,再利用余弦定理表示出cosC,根据C为三角形的内角,可求角C的大小;
(2)c=2,可得a2+b2-ab=4,利用三角形的面积公式,可得ab=4,即可求出a,b的值.
(2)c=2,可得a2+b2-ab=4,利用三角形的面积公式,可得ab=4,即可求出a,b的值.
解答:
解:∵sin2A+sin2B+cos2C=1+sinAsinB
∴sin2A+sin2B-sinAsinB=sin2C,
利用正弦定理化简得:a2+b2-ab=c2,即a2+b2-c2=ab,
∴根据余弦定理得:cosC=
=
,
∵C为三角形的内角,
∴C=
;
(2)∵c=2,
∴a2+b2-ab=4①,
∵△ABC的面积为
,
∴S△ABC=
ab•sinC=
,
∴ab=4②,
∴由①②可得a=b=2.
∴sin2A+sin2B-sinAsinB=sin2C,
利用正弦定理化简得:a2+b2-ab=c2,即a2+b2-c2=ab,
∴根据余弦定理得:cosC=
| a2+b2-c2 |
| 2ab |
| 1 |
| 2 |
∵C为三角形的内角,
∴C=
| π |
| 3 |
(2)∵c=2,
∴a2+b2-ab=4①,
∵△ABC的面积为
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 3 |
∴ab=4②,
∴由①②可得a=b=2.
点评:此题考查了正弦、余弦定理,三角形的面积公式,正弦、余弦定理很好的建立了三角形的边角关系,熟练掌握定理是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
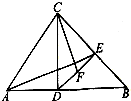 如图,在锐角三角形ABC中,D为C在AB上的射影,E为D在BC上的射影,F为DE上一点,且满足
如图,在锐角三角形ABC中,D为C在AB上的射影,E为D在BC上的射影,F为DE上一点,且满足 如图AB是⊙O的直径,P为AB延长线上一点,PC切⊙O于点C,PC=4,PB=2.则⊙O的半径等于
如图AB是⊙O的直径,P为AB延长线上一点,PC切⊙O于点C,PC=4,PB=2.则⊙O的半径等于