题目内容
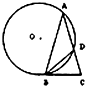如图，△ABC中AB=AC，∠ABC=72°，圆O过A，B且与BC切于B点，与AC交于D点，连BD．若BC=2，则AC=考点：与圆有关的比例线段
专题：选作题,立体几何
分析：利用切割线定理，可得BC2=（AC-BC）•AC，即可求出AC的值．
解答：
解：∵AB=AC，∠C=72°，BC是⊙O的切线，
∴∠CBD=∠BAC=36°，
∴∠ABD=36°，
∴∠BDC=∠BCD=72°，
∴AD=BD=BC；
又∵BC是切线，
∴BC2=CD•AC，
∴BC2=（AC-BC）•AC
设AC=x，则可得到：（x-2）x=4，
∴x2-2x-4=0
解得：x1=1+
，x2=1-
（x2＜0不合题意，舍去）．
∴AC=1+
．
故答案为：1+
．
∴∠CBD=∠BAC=36°，
∴∠ABD=36°，
∴∠BDC=∠BCD=72°，
∴AD=BD=BC；
又∵BC是切线，
∴BC2=CD•AC，
∴BC2=（AC-BC）•AC
设AC=x，则可得到：（x-2）x=4，
∴x2-2x-4=0
解得：x1=1+
| 5 |
| 5 |
∴AC=1+
| 5 |
故答案为：1+
| 5 |
点评：本题考查切线的性质定理，切割线定理，考查解一元二次方程，属于中档题．
练习册系列答案
相关题目
如图AB是⊙O的直径，P为AB延长线上一点，PC切⊙O于点C，PC=4，PB=2．则⊙O的半径等于