题目内容
已知函数f(x)=|x+1|+|x-3|.
(1)求不等式f(x)<6的解集;
(2)若关于x的方程f(x)=|a-2|有解,求实数a的取值范围.
(1)求不等式f(x)<6的解集;
(2)若关于x的方程f(x)=|a-2|有解,求实数a的取值范围.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(1)原不等式等价于
或
或
<0,分别解每一个不等式,最后取其并集即可;
(2)利用绝对值不等式可得f(x)=|x+1|+|x-3|≥|x+1-x-3|=4,依题意,解不等式|a-2|≥4即可求得实数a的取值范围.
|
|
|
(2)利用绝对值不等式可得f(x)=|x+1|+|x-3|≥|x+1-x-3|=4,依题意,解不等式|a-2|≥4即可求得实数a的取值范围.
解答:
解:(1)原不等式等价于
或
或
<0…(3分)
解得-2<x<-1或-1≤x≤3或3<x<4,
故原不等式的解集为{x|-2<x<4}.…(5分)
(2)∵f(x)=|x+1|+|x-3|≥|x+1-x-3|=4.…(7分)
又关于x的方程f(x)=|a-2|有解,
∴|a-2|≥4,即a-2≥4或a-2≤-4,解得a≥6或a≤-2,…(9分)
所以实数a的取值范围为a≥6或a≤-2.…(10分)
|
|
|
解得-2<x<-1或-1≤x≤3或3<x<4,
故原不等式的解集为{x|-2<x<4}.…(5分)
(2)∵f(x)=|x+1|+|x-3|≥|x+1-x-3|=4.…(7分)
又关于x的方程f(x)=|a-2|有解,
∴|a-2|≥4,即a-2≥4或a-2≤-4,解得a≥6或a≤-2,…(9分)
所以实数a的取值范围为a≥6或a≤-2.…(10分)
点评:本题考查绝对值不等式的解法,考查分类讨论思想与等价转化思想的综合运用,考查解不等式的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
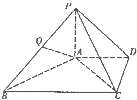 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,BC=2AD,PB⊥AC,Q是线段PB的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,BC=2AD,PB⊥AC,Q是线段PB的中点.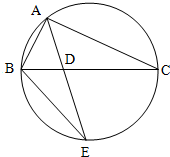 如图所示,圆的两条弦AE,BC交于点D,且
如图所示,圆的两条弦AE,BC交于点D,且