题目内容
现有0,1,2,3,4,5六个数字.
(1)用所给数字能够组成多少个四位数?
(2)用所给数字可以组成多少个没有重复数字的五位数?
(3)用所给数字可以组成多少个没有重复数字且比3142大的数?(最后结果均用数字作答)
(1)用所给数字能够组成多少个四位数?
(2)用所给数字可以组成多少个没有重复数字的五位数?
(3)用所给数字可以组成多少个没有重复数字且比3142大的数?(最后结果均用数字作答)
考点:计数原理的应用
专题:排列组合
分析:(1)利用分步计数原理,第一步先排首位(因为零不能再首位),再排其它三个位值,注意数字可以重复,
(2)利用分步计数原理,第一步先排首位(因为零不能再首位),再排其它四个位值,注意数字不可以重复,
(3)利用分类计数原理,比3142大的数包含四位数、五位数和六位数,然后再分类求出即可.
(2)利用分步计数原理,第一步先排首位(因为零不能再首位),再排其它四个位值,注意数字不可以重复,
(3)利用分类计数原理,比3142大的数包含四位数、五位数和六位数,然后再分类求出即可.
解答:
解:(1)能够组成四位数的个数为:5×6×6×6=1080
(2)能组成没有重复数字的五位数的个数为:
=600;
(3)比3142大的数包含四位数、五位数和六位数,其中:
六位数有:
•
=5×5×4×3×2×1=600;
五位数有:
=600;
四位数有千位是4或5的,千位是3的,而千位是4或5的有
•
=2×5×4×3=120;
千位是3的分为百位是2、4、5的与百位是1的,
百位是2、4、5的有
•
=3×4×3=36,
百位是1的分为十位是4和5两种情况,十位是5的有3种,十位是4的有1种,
所以共有600+600+120+36+3+1=1360.
答:能组成四位数1080个;没有重复数字的五位数600个;比3142大的数1360个.
(2)能组成没有重复数字的五位数的个数为:
| A | 1 5 |
| •A | 4 5 |
(3)比3142大的数包含四位数、五位数和六位数,其中:
六位数有:
| C | 1 5 |
| A | 5 5 |
五位数有:
| A | 1 5 |
| •A | 4 5 |
四位数有千位是4或5的,千位是3的,而千位是4或5的有
| C | 1 2 |
| A | 3 5 |
千位是3的分为百位是2、4、5的与百位是1的,
百位是2、4、5的有
| C | 1 3 |
| A | 2 4 |
百位是1的分为十位是4和5两种情况,十位是5的有3种,十位是4的有1种,
所以共有600+600+120+36+3+1=1360.
答:能组成四位数1080个;没有重复数字的五位数600个;比3142大的数1360个.
点评:本题主要考查了分类计数原理,关键如何分类,遵循不重不漏的原则,属于中档题.

练习册系列答案
相关题目
 如图,在四棱锥S-ABCD中,底面ABCD是矩形,AD=2AB,SA=SD,SA⊥AB,N是棱AD的中点.
如图,在四棱锥S-ABCD中,底面ABCD是矩形,AD=2AB,SA=SD,SA⊥AB,N是棱AD的中点.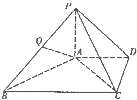 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,BC=2AD,PB⊥AC,Q是线段PB的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,BC=2AD,PB⊥AC,Q是线段PB的中点.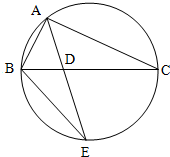 如图所示,圆的两条弦AE,BC交于点D,且
如图所示,圆的两条弦AE,BC交于点D,且