题目内容
15.在空间直角坐标系Oxyz中,已知$A(2,0,0),B(2,2,0),C(0,2,0),D(1,1,\sqrt{2})$,则直线AD与平面ABC所成的角为( )| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
分析 求出平面ABC的法向量,利用向量法能求出直线AD与平面ABC所成的角的大小.
解答 解:∵在空间直角坐标系Oxyz中,
$A(2,0,0),B(2,2,0),C(0,2,0),D(1,1,\sqrt{2})$,
∴$\overrightarrow{AD}$=(-1,1,$\sqrt{2}$),$\overrightarrow{AB}$=(0,2,0),$\overrightarrow{AC}$=(-2,2,0),
设平面ABC的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AB}=2y=0}\\{\overrightarrow{n}•\overrightarrow{AC}=-2x+2y=0}\end{array}\right.$,∴$\overrightarrow{n}$=(0,0,1)
设直线AD与平面ABC所成的角为θ,
sinθ=$\frac{|\overrightarrow{n}•\overrightarrow{AD}|}{|\overrightarrow{n}|•|\overrightarrow{AD}|}$=$\frac{|\sqrt{2}|}{1×\sqrt{4}}$=$\frac{\sqrt{2}}{2}$,
∴θ=45°,
∴直线AD与平面ABC所成的角为45°.
故选:C.
点评 本题考查线面角的大小的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
3.已知集合A={1,m2},B={0,4},则“m=-2”是“A∩B={4}”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
10.已知四边形ABCD是平行四边形,对角线相交于点O,则下列等式中成立的是( )
| A. | $\overrightarrow{BC}$+$\overrightarrow{BA}$=$\overrightarrow{AC}$ | B. | $\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{BC}$ | C. | $\overrightarrow{AO}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AD}$) | D. | $\overrightarrow{AD}$=$\overrightarrow{CB}$ |
7.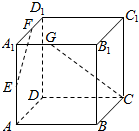 如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AA1,A1D1,A1B1的中点,则异面直线EF与CG所成的角等于( )
如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AA1,A1D1,A1B1的中点,则异面直线EF与CG所成的角等于( )
 如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AA1,A1D1,A1B1的中点,则异面直线EF与CG所成的角等于( )
如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AA1,A1D1,A1B1的中点,则异面直线EF与CG所成的角等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
5.在区间[-5,5]内随机地取出一个数a,使得1∈{x|2x2+ax-a2>0}的概率为( )
| A. | $\frac{3}{10}$ | B. | $\frac{3}{20}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{2}$ |