已知四边形ABCD是平行四边形.对角线相交于点O.则下列等式中成立的是( )A．$\overrightarrow{BC}$+$\overrightarrow{BA}$=$\overrightarrow{AC}$B．$\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{BC}$C．$\overrightarrow{AO}$= 题目和参考答案——青夏教育精英家教网—

题目内容

10．已知四边形ABCD是平行四边形，对角线相交于点O，则下列等式中成立的是（　　）

A．

$\overrightarrow{BC}$+$\overrightarrow{BA}$=$\overrightarrow{AC}$

B．

$\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{BC}$

C．

$\overrightarrow{AO}$=$\frac{1}{2}$（$\overrightarrow{AB}$+$\overrightarrow{AD}$）

D．

$\overrightarrow{AD}$=$\overrightarrow{CB}$

分析根据向量的加减的几何意义和三角形法则，平行四边形法则判断即可．

解答解：四边形ABCD是平行四边形，对角线相交于点O，
∴$\overrightarrow{AO}$=$\frac{1}{2}$（$\overrightarrow{AB}$+$\overrightarrow{AD}$），$\overrightarrow{BC}+\overrightarrow{BA}$=$\overrightarrow{BD}$，$\overrightarrow{AB}$$-\overrightarrow{AC}$=$\overrightarrow{CB}$，$\overrightarrow{AD}$=-$\overrightarrow{CB}$，
故A，B，D不正确，C正确．
故选：C．

点评本题考查了向量的加减的几何意义，属于基础题．

练习册系列答案

相关题目

11．已知函数f（x）=（a+2）x^-2是幂函数，则f（a）的值为（　　）

1．下列各项中的对象不能组成集合的是（3）
（1）所有的直角三角形
（2）数学《必修1》教材中所有的习题
（3）所有数学难题
（4）所有无理数．

18．已知函数f（x）=2sin（3x+2φ）为偶函数，则φ的最小正值为$\frac{π}{4}$．

5．下列结论中，正确的是（　　）

	A．	三角形绕其一边旋转一周后成一个圆锥
	B．	一个直角梯形绕其一边旋转一周后成为一个圆台
	C．	平行四边形绕其一边旋转一周后成为圆柱
	D．	圆面绕其一条直径旋转一周后成为一个球

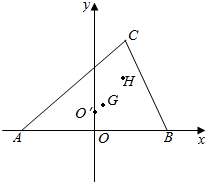15．在空间直角坐标系Oxyz中，已知$A（2，0，0），B（2，2，0），C（0，2，0），D（1，1，\sqrt{2}）$，则直线AD与平面ABC所成的角为（　　）

2．

如图，A，B，C的坐标分别为（-$\frac{c}{2}$，0），（$\frac{c}{2}$，0），（m，n），G，O′，H分别为△ABC的重心，外心，垂心．
（1）写出重心G的坐标；
（2）求外心O′，垂心H的坐标；
（3）求证：G，H，O′三点共线，且满足|GH|=2|OG′|．

19．某工厂接到一任务，需加工6000个P型零件和2000个Q型零件．这个厂有214名工人，他们每一个人用以加工5个P型零件的时间可以加工3个Q型零件，将这些工人分成两组同时工作，每组加工一种型号的零件．为了在最短时间内完成这批任务，则加工P型零件的人数为137人．

20．已知△ABC的三个顶点的坐标为A（1，0），B（3，2），C（2，4）．求：
（1）点D的坐标，使四边形ABCD是平行四边形；
（2）点C关于直线AB对称点的坐标；
（3）△ABC的面积．

试题分类