题目内容
6.已知圆 C:x2+y2+2x-4y+3=0(1)求圆心C的坐标及半径r的大小;
(2)从圆外一点 P(x,y)向圆引一条切线,切点为 M,O为坐标原点,且有|MP|=|OP|,求动点P的轨迹方程.
分析 (1)利用配方法求出圆的标准方程即可求出圆的圆心与半径.
(2)设出P的坐标,利用垂直条件列出方程,求解即可.
解答  解:(1)圆的标准方程为(x+1)2+(y-2)2=2,
解:(1)圆的标准方程为(x+1)2+(y-2)2=2,
则圆心C(-1,2),半径r=$\sqrt{2}$.
(2)由题如图,PM与圆C相切于M,∴PM⊥CM
设P(x,y),由MP=OP得:OP2=MP2=CP2-r2
∴x2+y2=(x+1)2+(y-2)2-2
整理得:2x-4y+3=0即为所求.
点评 本题考查轨迹方程的求法,利用圆的标准方程求出圆心和半径是解决本题的关键.考查计算能力.

练习册系列答案
相关题目
8.已知函数f(x)=$\left\{\begin{array}{l}{2sin\frac{π}{6}x,x≤2000}\\{x-1000,x>2000}\end{array}\right.$,则f(f(2016))=( )
| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | 1 | D. | -1 |
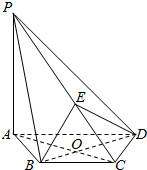 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD于O,E为线段PC上一点,且AC⊥BE,
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD于O,E为线段PC上一点,且AC⊥BE,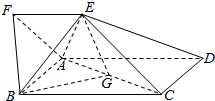 如图,四边形ABCD为矩形,四边形ADEF为梯形,AD∥FE,∠AFE=60°,且平面ABCD⊥平面ADEF,AF=FE=AB=$\frac{1}{2}AD$=2,点G为AC的中点.
如图,四边形ABCD为矩形,四边形ADEF为梯形,AD∥FE,∠AFE=60°,且平面ABCD⊥平面ADEF,AF=FE=AB=$\frac{1}{2}AD$=2,点G为AC的中点.