题目内容
20.已知曲线C的参数方程为$\left\{\begin{array}{l}{x=-1+cosθ}\\{y=1+sinθ}\end{array}\right.$(θ为参数),则曲线C的普通方程是(x+1)2+(y-1)2=1.点A是曲线C的对称中心,点P(x,y)在不等式x+y≥2所表示的平面区域内,则|AP|的取值范围是[$\sqrt{2}$,+∞).分析 首先,直接根据参数方程化为普通方程的思路,消去参数即可得到相应的普通方程;然后,根据圆的对称性,得到点A的坐标,结合图形,得到相应的距离就是最小值,从而得到相应的取值范围.
解答 解:根据曲线C的参数方程为$\left\{\begin{array}{l}{x=-1+cosθ}\\{y=1+sinθ}\end{array}\right.$(θ为参数),
消去参数θ,得
(x+1)2+(y-1)2=1,
∴该曲线C对应的普通方程为:(x+1)2+(y-1)2=1,
结合圆的性质,得A(-1,1),如图所示:
|AP|的最小值为点A到直线x+y-2=0的距离,
即此时距离为d=$\frac{|-1+1-2|}{\sqrt{1+1}}$=$\sqrt{2}$,
∴则|AP|的取值范围是[$\sqrt{2}$,+∞).
故答案为:(x+1)2+(y-1)2=1[$\sqrt{2}$,+∞).
点评 本题重点考查了圆的参数方程和普通方程的互化、数形结合思想、点到直线的距离公式等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.总体由编号为00,01,02,…,19的20个个体组成,利用下面给出的随机数表从20个个体中选取5个个体,选取方法是从随机数表第一行的第5列数字开始由左到右依次选定两个数字,则选出来的第5个个体编号为( )
| 78 | 16 | 95 | 72 | 08 | 14 | 07 | 43 | 63 | 42 | 03 | 20 | 97 | 28 | 01 | 98 |
| 32 | 04 | 92 | 34 | 49 | 35 | 82 | 40 | 36 | 23 | 48 | 69 | 69 | 38 | 74 | 81 |
| A. | 01 | B. | 07 | C. | 08 | D. | 20 |
15.在空间直角坐标系Oxyz中,已知$A(2,0,0),B(2,2,0),C(0,2,0),D(1,1,\sqrt{2})$,则直线AD与平面ABC所成的角为( )
| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
5.(重点中学做)“x<-1”是“ln(x+2)<0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
12.(普通中学做)已知数列{an}满足a1+3a2+5a3+…+(2n-1)an=(n-1)3n+1+3(n∈N*),则数列{an}的前n项和Sn=$\frac{3}{2}({3}^{n}-1)$.
9.在直三棱柱ABC-A1B1C1中,AB⊥BC,AB=BC=AA1,则异面直线AC1与B1C所成角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
10.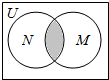 已知全集U=R,集合M={x|-1≤x≤3}和集合N={x|x=2k-1,k∈N}的关系的韦恩(Venn)图如图所示,则阴影部分所示的集合为( )
已知全集U=R,集合M={x|-1≤x≤3}和集合N={x|x=2k-1,k∈N}的关系的韦恩(Venn)图如图所示,则阴影部分所示的集合为( )
 已知全集U=R,集合M={x|-1≤x≤3}和集合N={x|x=2k-1,k∈N}的关系的韦恩(Venn)图如图所示,则阴影部分所示的集合为( )
已知全集U=R,集合M={x|-1≤x≤3}和集合N={x|x=2k-1,k∈N}的关系的韦恩(Venn)图如图所示,则阴影部分所示的集合为( )| A. | {x|-1≤x≤3} | B. | {-3,-1,1,3,5} | C. | {-1,1,3} | D. | {-1,1,3,5} |
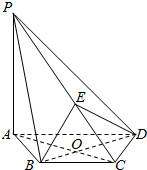 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD于O,E为线段PC上一点,且AC⊥BE,
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD于O,E为线段PC上一点,且AC⊥BE,