题目内容
5.在区间[-5,5]内随机地取出一个数a,使得1∈{x|2x2+ax-a2>0}的概率为( )| A. | $\frac{3}{10}$ | B. | $\frac{3}{20}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{2}$ |
分析 由1∈{x|2x2+ax-a2>0}代入得出关于参数a的不等式,解之求得a的范围,再由几何的概率模型的知识求出其概率.
解答 解:由题意1∈{x|2x2+ax-a2>0},故有2+a-a2>0,解得-1<a<2
由几何概率模型的知识知,总的测度,区间[-5,5]的长度为10,随机地取出一个数a,使得1∈{x|2x2+ax-a2>0}这个事件的测度为3
故区间[-5,5]内随机地取出一个数a,使得1∈{x|2x2+ax-a2>0}的概率为$\frac{3}{10}$.
故选:A.
点评 本题考查几何概率模型,求解本题的关键是正确理解1∈{x|2x2+ax-a2>0}的意义,即得到参数a所满足的不等式,从中解出事件所对应的测度.

练习册系列答案
相关题目
15.在空间直角坐标系Oxyz中,已知$A(2,0,0),B(2,2,0),C(0,2,0),D(1,1,\sqrt{2})$,则直线AD与平面ABC所成的角为( )
| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
10.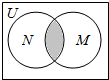 已知全集U=R,集合M={x|-1≤x≤3}和集合N={x|x=2k-1,k∈N}的关系的韦恩(Venn)图如图所示,则阴影部分所示的集合为( )
已知全集U=R,集合M={x|-1≤x≤3}和集合N={x|x=2k-1,k∈N}的关系的韦恩(Venn)图如图所示,则阴影部分所示的集合为( )
 已知全集U=R,集合M={x|-1≤x≤3}和集合N={x|x=2k-1,k∈N}的关系的韦恩(Venn)图如图所示,则阴影部分所示的集合为( )
已知全集U=R,集合M={x|-1≤x≤3}和集合N={x|x=2k-1,k∈N}的关系的韦恩(Venn)图如图所示,则阴影部分所示的集合为( )| A. | {x|-1≤x≤3} | B. | {-3,-1,1,3,5} | C. | {-1,1,3} | D. | {-1,1,3,5} |
17.已知集合M={x|$\frac{x-2}{x+1}$<0},N={x|x≤-1},则集合{x|x≥2}等于( )
| A. | M∩N | B. | M∪N | C. | ∁R(M∩N) | D. | ∁R(M∪N) |
14.阅读程序框图,为使输出的数据为31,则①处应填的表达式为( )


| A. | i≤3 | B. | i≤4 | C. | i≤5 | D. | i≤6 |
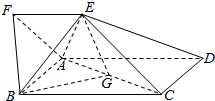 如图,四边形ABCD为矩形,四边形ADEF为梯形,AD∥FE,∠AFE=60°,且平面ABCD⊥平面ADEF,AF=FE=AB=$\frac{1}{2}AD$=2,点G为AC的中点.
如图,四边形ABCD为矩形,四边形ADEF为梯形,AD∥FE,∠AFE=60°,且平面ABCD⊥平面ADEF,AF=FE=AB=$\frac{1}{2}AD$=2,点G为AC的中点.