题目内容
4.已知圆C:x2+y2-4x-5=0.(Ⅰ)判断圆C与圆D:(x-5)2+(y-4)2=4的位置关系,并说明理由;
(Ⅱ)若过点(5,4)的直线l与圆C相切,求直线l的方程.
分析 (Ⅰ)利用圆C与圆D的连心线长=圆C与圆D的两半径之和,判断圆C与圆D:(x-5)2+(y-4)2=4的位置关系;
(Ⅱ)分类讨论,利用圆心C(2,0)到直线l的距离=半径,求直线l的方程.
解答 解:(Ⅰ)∵圆C的标准方程是(x-2)2+y2=9
∴圆C的圆心坐标是(2,0),半径长r1=3…(2分)
又圆D的圆心坐标是(5,4),半径长r2=2
∴圆C与圆D的连心线长为$\sqrt{{{(2-5)}^2}+{{(0-4)}^2}}=5$…(4分)
又圆C与圆D的两半径之和为r1+r2=5
∴圆C与圆D外切…(5分)
(Ⅱ)当直线l的斜率不存在时,直线l的方程为x=5,符合题意 …(7分)
当直线l的斜率存在时,设直线l的方程为y=k(x-5)+4,即kx-y+4-5k=0
∵直线l与圆C相切
∴圆心C(2,0)到直线l的距离d=3,即$d=\frac{{|{2k+4-5k}|}}{{\sqrt{{k^2}+1}}}=3$,解得$k=\frac{7}{24}$…(10分)
∴此时直线l的方程为$\frac{7}{24}x-y+4-\frac{35}{24}=0$,即7x-24y+61=0…(11分)
综上,直线l的方程为x=5或7x-24y+61=0…(12分)
点评 本题考查圆与圆的位置关系,考查直线与圆的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
15.在空间直角坐标系Oxyz中,已知$A(2,0,0),B(2,2,0),C(0,2,0),D(1,1,\sqrt{2})$,则直线AD与平面ABC所成的角为( )
| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
12.(普通中学做)已知数列{an}满足a1+3a2+5a3+…+(2n-1)an=(n-1)3n+1+3(n∈N*),则数列{an}的前n项和Sn=$\frac{3}{2}({3}^{n}-1)$.
9.在直三棱柱ABC-A1B1C1中,AB⊥BC,AB=BC=AA1,则异面直线AC1与B1C所成角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
14.阅读程序框图,为使输出的数据为31,则①处应填的表达式为( )


| A. | i≤3 | B. | i≤4 | C. | i≤5 | D. | i≤6 |
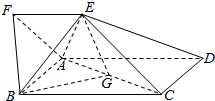 如图,四边形ABCD为矩形,四边形ADEF为梯形,AD∥FE,∠AFE=60°,且平面ABCD⊥平面ADEF,AF=FE=AB=$\frac{1}{2}AD$=2,点G为AC的中点.
如图,四边形ABCD为矩形,四边形ADEF为梯形,AD∥FE,∠AFE=60°,且平面ABCD⊥平面ADEF,AF=FE=AB=$\frac{1}{2}AD$=2,点G为AC的中点.