题目内容
已知集合A={1，x，x2-x}，B={1，2，x}，若集合A与集合B相等，求x的值．
考点：集合的相等
专题：集合
分析：集合A与集合B相等，由于x2-x≠x，x2-x≠1．可得x2-x=2．解得x，再进行验证即可．
解答：
解：∵集合A与集合B相等，∴x2-x≠x，x2-x≠1．
∴x2-x=2．解得x=2或x=-1．
当x=2时，与集合元素的互异性矛盾．
当x=-1时，符合题意．
∴x=-1．
∴x2-x=2．解得x=2或x=-1．
当x=2时，与集合元素的互异性矛盾．
当x=-1时，符合题意．
∴x=-1．
点评：本题考查了集合相等、集合元素的性质、分类讨论，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
直线y=ax+b过第一、三、四象限，则圆（x+a）2+（y+b）2=r2（r＞0）的圆心在（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
掷两颗均匀的大小不同的骰子，记“两颗骰子的点数和为10”为事件A，“小骰子出现的点数大于大骰子出现的点数”为事件B，则P（B|A）为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
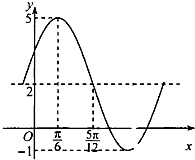已知函数f（x）=Asin（ωx+φ）+b（A、ω＞0，0＜φ＜π，b为常数）一段图象如图所示．
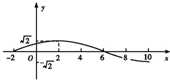已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜