Question

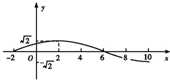已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜

π

2

）的部分图象如图所示
（1）求函数f（x）的解析式并写出其对称中心；
（2）若g（x）的图象与f（x）的图象关于直线x=4对称，当x∈[2，8]，求g（x）的最大值和最小值．

Answer 1

考点：函数y=Asin（ωx+φ）的图象变换,余弦函数的图象

专题：计算题,综合题,三角函数的图像与性质

分析：（1）由图知，A=

2

，

1

2

T=8，从而可求得ω，又函数f（x）=Asin（ωx+φ）的图象经过点（-2，0），于是可求得φ，继而可得函数f（x）的解析式，利用其对称性可写出其对称中心；
（2）设g（x）的图象上任意点（x，g（x）），依题意，g（x）=f（8-x）=

2

sin（

5π

4

-

π

8

x），x∈[2，8]⇒

π

4

≤

5π

4

-

π

8

x≤π，利用正弦函数的单调性与最值，可求得
y=g（x）的值域，从而可得其最值．

解答： 解：（1）由图知，A=

2

，

1

2

T=6-（-2）=8，
∴T=

2π

ω

=16，
解得：ω=

π

8

；
又函数f（x）=Asin（ωx+φ）的图象经过点（-2，0），
∴-2×

π

8

+φ=2kπ（k∈Z），
∴φ=2kπ+

π

4

（k∈Z），又|φ|＜

π

2

，
∴φ=

π

4

，
∴f（x）=

2

sin（

π

8

x+

π

4

）；
由

π

8

x+

π

4

=kπ（k∈Z）得：x=8k-2（k∈Z），
∴函数f（x）的对称中心为（8k-2，0）（k∈Z）；
（2）设g（x）的图象上任意点（x，g（x）），
它关于直线x=4的对称点（8-x，g（x））在y=f（x）的图象上，
∴g（x）=f（8-x）=

2

sin[

π

8

（8-x）+

π

4

]=

2

sin（

5π

4

-

π

8

x），
∵x∈[2，8]，
∴

π

4

≤

π

8

x≤π，-π≤-

π

8

x≤-

π

4

，

π

4

≤

5π

4

-

π

8

x≤π，
∴sin[

π

8

（8-x）+

π

4

]∈[0，1]，
∴

2

sin[

π

8

（8-x）+

π

4

]∈[0，

2

]，即g（x）∈[0，

2

]，
∴g（x）_max=

2

，g（x）_min=0．

点评：本题考查函数y=Asin（ωx+φ）的图象变换，考查函数的对称性，突出考查正弦函数的单调性，考查转化思想与运算求解能力，属于中档题．