Question

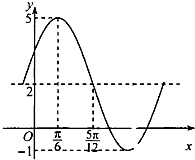已知函数f（x）=Asin（ωx+φ）+b（A、ω＞0，0＜φ＜π，b为常数）一段图象如图所示．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）将函数y=f（x）的图象向左平移

π

12

个单位，再将所得图象上各点的横坐标扩大为原来的4倍，得到函数y=g（x）的图象．求函数g（x）的单调递增区间．

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式,函数y=Asin（ωx+φ）的图象变换

专题：三角函数的图像与性质

分析：（Ⅰ）由函数的最值求出A，由周期求出ω，由五点法作图求出φ的值，即可求得函数的解析式．
（Ⅱ）根据函数y=Asin（ωx+φ）的图象变换规律求得g（x）的解析式，再根据正弦函数的单调性求得g（x）的增区间．

解答： 解：（Ⅰ）由已知可得，A=5-2=3，b=

5+(-1)

2

=2，因为T=(

5π

12

-

π

6

)×4=π，所以ω=2．
由“五点法”作图，

π

6

×2+φ=

π

2

，解得φ=

π

6

．
所以函数f（x）的解析式为f(x)=3sin(2x+

π

6

)+2．  
（Ⅱ）将函数y=f（x）的图象向左平移

π

12

个单位后，
得到的函数解析式为y=3sin[2(x+

π

12

)+

π

6

]+2，即y=3sin(2x+

π

3

)+2．
再将图象上各点的横坐标扩大为原来的4倍，得g(x)=3sin(

1

2

x+

π

3

)+2．
由2kπ-

π

2

≤

1

2

x+

π

3

≤2kπ+

π

2

，得4kπ-

5π

3

≤x≤4kπ+

π

3

，
可得g（x）的单调递增区间为[4kπ-

5π

3

 ， 4kπ+

π

3

]，k∈Z．

点评：本题主要考查由函数y=Asin（ωx+φ）的部分图象求解析式，函数y=Asin（ωx+φ）的图象变换规律，正弦函数的单调性，属于中档题．